SVM: maszyna wektora wsparcia
Wcześniej przedstawiliśmy ideę granic decyzji i zauważyliśmy, że problemy, w których granica decyzji nie jest liniowa, stanowią problem dla prostych algorytmów klasyfikacji. Pokazaliśmy, jak wykonać regresję logistyczną, algorytm klasyfikacji, który działa poprzez konstruowanie liniowej granicy decyzji. I w obu rozdziałach obiecaliśmy opisać technikę zwaną sztuczką jądra, która może być użyta do rozwiązania problemów z nieliniowymi granicami decyzyjnymi. Złóżmy tę obietnicę, wprowadzając nowy algorytm klasyfikacji zwany maszyną wektorów wsparcia (SVM skrótowo), który pozwala używać wielu różnych jąder do znajdowania nieliniowych granic decyzyjnych. Użyjemy SVM do klasyfikacji punktów z zestawu danych z nieliniową granicą decyzji. W szczególności będziemy pracować z zestawem danych pokazanym na rysunku poniżej. Patrząc na ten zestaw danych, powinno być jasne, że punkty z klasy 0 znajdują się na obrzeżach, podczas gdy punkty z klasy 1 znajdują się w centrum wykresu. Tego rodzaju nieliniowej granicy decyzji nie można odkryć za pomocą prostego algorytmu klasyfikacji, takiego jak algorytm regresji logistycznej, który opisaliśmy wcześniej. Pokażmy to, próbując zastosować regresję logistyczną za pomocą funkcji glm. Następnie przeanalizujemy przyczynę niepowodzenia regresji logistycznej.
df <- read.csv(‘data/df.csv’)
logit.fit <- glm(Label ~ X + Y,
family = binomial(link = ‘logit’),
data = df)
logit.predictions <- ifelse(predict(logit.fit) > 0, 1, 0)
mean(with(df, logit.predictions == Label))
#[1] 0.5156
Jak widać, poprawnie przewidzieliśmy klasę tylko 52% danych. Ale moglibyśmy zrobić dokładnie to dobrze, przewidując, że każdy punkt danych należy do klasy 0:
mean(with(df, 0 == Label))
#[1] 0.5156
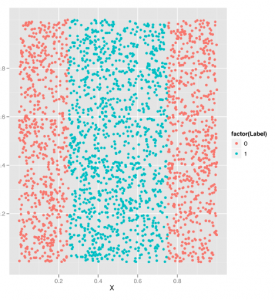
Krótko mówiąc, model regresji logistycznej (i znaleziona liniowa granica decyzji) jest całkowicie bezużyteczny. Dokonuje takich samych przewidywań jak model bez żadnych informacji poza faktem, że klasa 0 występuje częściej niż klasa 1, a zatem powinna być stosowana jako prognoza w przypadku braku wszystkich innych informacji. Jak więc możemy zrobić lepiej? Jak zobaczysz za chwilę, SVM zapewnia trywialny sposób i przewyższa regresję logistyczną. Zanim opiszemy, jak to robi, pokażemy, że działa jak algorytm czarnej skrzynki, który daje użyteczne odpowiedzi. Aby to zrobić, użyjemy pakietu e1071, który udostępnia funkcję svm, która jest równie łatwa w użyciu jak glm:
library(‘e1071’)
svm.fit <- svm(Label ~ X + Y, data = df)
svm.predictions <- ifelse(predict(svm.fit) > 0, 1, 0)
mean(with(df, svm.predictions == Label))
#[1] 0.7204
Tutaj wyraźnie osiągnęliśmy lepsze wyniki niż regresja logistyczna, przechodząc na SVM. Jak robi to SVM? Pierwszym sposobem na uzyskanie wglądu w doskonałą wydajność maszyny SVM jest wykreślenie jej prognoz w porównaniu z regresją logistyczną:
df <- cbind(df,
data.frame(Logit = ifelse(predict(logit.fit) > 0, 1, 0),
SVM = ifelse(predict(svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c(‘X’, ‘Y’))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)
Tutaj dodaliśmy prognozy regresji logistycznej i prognozy SVM do surowego zestawu danych. Następnie używamy funkcji stopu, aby zbudować zestaw danych, z którym łatwiej jest pracować do celów drukowania, i przechowujemy ten nowy zestaw danych w ramce danych zwanej prognozami. Następnie wykreślamy podstawowe etykiety prawdy wraz z przewidywaniami logit i SVM na fasetowanym wykresie pokazanym tu.
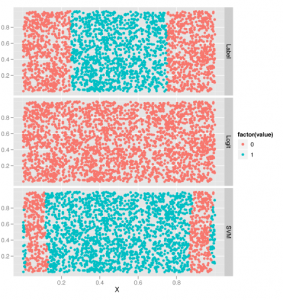
Gdy to zrobimy, staje się oczywiste, że regresja logistyczna jest bezużyteczna, ponieważ ustawia granicę decyzji poza zbiorem danych, podczas gdy dane dotyczące prawdziwości gruntu w górnym rzędzie wyraźnie zawierają zakres wpisów dla klasy 1 pośrodku. SVM jest w stanie uchwycić tę strukturę pasma, nawet jeśli dokonuje nieparzystych prognoz w pobliżu najdalszych granic zbioru danych. Teraz widzieliśmy, że SVM tworzy, zgodnie z obietnicą, nieliniową granicę decyzji. Ale jak to robi? Odpowiedź jest taka, że SVM używa sztuczki jądra. Za pomocą transformacji matematycznej przenosi oryginalny zestaw danych do nowej przestrzeni matematycznej, w której granice decyzji są łatwe do opisania. Ponieważ ta transformacja zależy tylko od prostego obliczenia obejmującego „jądra”, technika ta nazywa się sztuczką jądra. Opis matematyki sztuczki jądra nie jest prosty, ale łatwo jest uzyskać intuicję, testując różne jądra. Jest to łatwe, ponieważ funkcja SVM ma parametr o nazwie jądro, który można ustawić na jedną z czterech wartości: liniową, wielomianową, radialną i sigmoidalną. Aby dowiedzieć się, jak działają te jądra, spróbujmy użyć ich wszystkich do wygenerowania prognoz, a następnie wykreślić prognozy:
df <- df[, c(‘X’, ‘Y’, ‘Label’)]
linear.svm.fit <- svm(Label ~ X + Y, data = df, kernel = ‘linear’)
with(df, mean(Label == ifelse(predict(linear.svm.fit) > 0, 1, 0)))
polynomial.svm.fit <- svm(Label ~ X + Y, data = df, kernel = ‘polynomial’)
with(df, mean(Label == ifelse(predict(polynomial.svm.fit) > 0, 1, 0)))
radial.svm.fit <- svm(Label ~ X + Y, data = df, kernel = ‘radial’)
with(df, mean(Label == ifelse(predict(radial.svm.fit) > 0, 1, 0)))
sigmoid.svm.fit <- svm(Label ~ X + Y, data = df, kernel = ‘sigmoid’)
with(df, mean(Label == ifelse(predict(sigmoid.svm.fit) > 0, 1, 0)))
df <- cbind(df,
data.frame(LinearSVM = ifelse(predict(linear.svm.fit) > 0, 1, 0),
PolynomialSVM = ifelse(predict(polynomial.svm.fit) > 0, 1, 0),
RadialSVM = ifelse(predict(radial.svm.fit) > 0, 1, 0),
SigmoidSVM = ifelse(predict(sigmoid.svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c(‘X’, ‘Y’))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)
Jak widać na rysunku , jądra liniowe i wielomianowe przypominają mniej więcej regresję logistyczną.
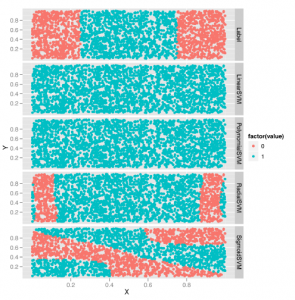
Natomiast jądro promieniowe daje nam granicę decyzyjną podobną do granicy prawdy naziemnej. Jądro sigmoidów daje nam bardzo złożoną i dziwną granicę decyzji. Powinieneś wygenerować własne zestawy danych i bawić się tymi czterema jądrami, aby zbudować intuicję dotyczącą ich działania. Po wykonaniu tej czynności możesz podejrzewać, że SVM może przewidywać znacznie lepsze przewidywania, niż wydaje się to po wyjęciu z pudełka. To prawda. SVM jest dostarczany z zestawem hiperparametrów, które domyślnie nie są ustawione na przydatne wartości, a uzyskanie najlepszych przewidywań z modelu wymaga dostrajania ich hiperparametry. Opiszmy główne hiperparametry i zobaczmy, jak ich tuning poprawia wydajność naszego modelu. Pierwszym hiperparametrem, z którym możesz pracować, jest stopień wielomianu używanego przez jądro wielomianu. Możesz to zmienić, ustawiając wartość stopnia podczas wywoływania svm. Zobaczmy, jak ten hiperparametr działa na czterech prostych przykładach:
polynomial.degree3.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘polynomial’,
degree = 3)
with(df, mean(Label != ifelse(predict(polynomial.degree3.svm.fit) > 0, 1, 0)))
#[1] 0.5156
polynomial.degree5.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘polynomial’,
degree = 5)
with(df, mean(Label != ifelse(predict(polynomial.degree5.svm.fit) > 0, 1, 0)))
#[1] 0.5156
polynomial.degree10.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘polynomial’,
degree = 10)
with(df, mean(Label != ifelse(predict(polynomial.degree10.svm.fit) > 0, 1, 0)))
#[1] 0.4388
polynomial.degree12.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘polynomial’,
degree = 12)
with(df, mean(Label != ifelse(predict(polynomial.degree12.svm.fit) > 0, 1, 0)))
#[1] 0.4464
Tutaj widzimy, że ustawienie stopnia na 3 lub 5 nie ma żadnego wpływu na jakość prognoz modelu. (Warto zauważyć, że domyślna wartość stopnia to 3.) Ale ustawienie stopnia na 10 lub 12 ma wpływ. Aby zobaczyć, co się dzieje, ponownie ustalmy granice decyzji:
df <- df[, c(‘X’, ‘Y’, ‘Label’)]
df <- cbind(df,
data.frame(Degree3SVM = ifelse(predict(polynomial.degree3.svm.fit) > 0,
1,
0),
Degree5SVM = ifelse(predict(polynomial.degree5.svm.fit) > 0,
1,
0),
Degree10SVM = ifelse(predict(polynomial.degree10.svm.fit) > 0,
1,
0),
Degree12SVM = ifelse(predict(polynomial.degree12.svm.fit) > 0,
1,
0)))
predictions <- melt(df, id.vars = c(‘X’, ‘Y’))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)
Patrząc na prognozy pokazane poniżej, widać wyraźnie, że użycie większego stopnia poprawia jakość prognoz, choć robi to w hacking sposób, który tak naprawdę nie naśladuje struktury danych.
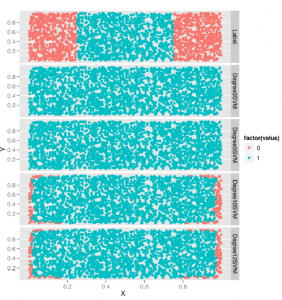
I, jak zauważysz, krok dopasowania modelu staje się coraz wolniejszy wraz ze wzrostem stopnia. I w końcu pojawią się te same problemy z nadmiernym dopasowaniem, które widzieliśmy w rozdziale 6 z regresją wielomianową. Z tego powodu należy zawsze używać weryfikacji krzyżowej w celu eksperymentowania z ustawianiem hiperparametru stopnia w aplikacjach korzystających z SVM z jądrem wielomianowym. Chociaż nie ma wątpliwości, że maszyny SVM z jądrem wielomianowym są cennym narzędziem w zestawie narzędzi, nie można zagwarantować, że będą działać dobrze bez wysiłku i myślenia z Twojej strony. Po zabawie z hiperparametrem stopnia dla jądra wielomianowego wypróbujmy hiperparametr kosztu, który jest stosowany we wszystkich możliwych jądrach SVM. Aby zobaczyć efekt zmiany kosztu, użyjemy jądra radialnego i wypróbujemy cztery różne ustawienia kosztów. Aby to zmienić, przestaniemy również zliczać błędy i zaczniemy sprawdzać, ile punktów danych przewidujemy poprawnie, ponieważ ostatecznie jesteśmy zainteresowani zobaczeniem, jak dobry jest najlepszy model, a nie, jak zły jest najgorszy model. Poniżej przedstawiono kod tego badania parametru kosztu:
radial.cost1.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘radial’,
cost = 1)
with(df, mean(Label == ifelse(predict(radial.cost1.svm.fit) > 0, 1, 0)))
#[1] 0.7204
radial.cost2.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘radial’,
cost = 2)
with(df, mean(Label == ifelse(predict(radial.cost2.svm.fit) > 0, 1, 0)))
#[1] 0.7052
radial.cost3.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘radial’,
cost = 3)
with(df, mean(Label == ifelse(predict(radial.cost3.svm.fit) > 0, 1, 0)))
#[1] 0.6996
radial.cost4.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘radial’,
cost = 4)
with(df, mean(Label == ifelse(predict(radial.cost4.svm.fit) > 0, 1, 0)))
#[1] 0.694
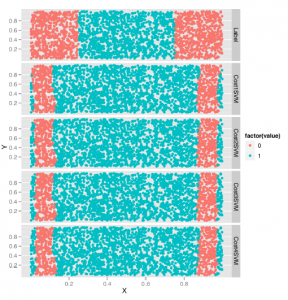
Jak widać, zwiększenie parametru kosztu powoduje, że model stopniowo dopasowuje się coraz bardziej i gorzej. Jest tak, ponieważ koszt jest hiperparametrem regularyzacji, takim jak parametr lambda, który opisaliśmy wcześniej, a jego zwiększenie zawsze sprawi, że model będzie mniej pasował do danych treningowych. Oczywiście ten wzrost regularyzacji może poprawić wydajność twojego modelu na danych testowych, więc zawsze powinieneś zobaczyć, jaka wartość kosztu najbardziej poprawia wydajność testu przy użyciu weryfikacji krzyżowej. Aby uzyskać wgląd w to, co się dzieje pod względem dopasowanego modelu, spójrzmy na przewidywania graficznie:
df <- df[, c(‘X’, ‘Y’, ‘Label’)]
df <- cbind(df,
data.frame(Cost1SVM = ifelse(predict(radial.cost1.svm.fit) > 0, 1, 0),
Cost2SVM = ifelse(predict(radial.cost2.svm.fit) > 0, 1, 0),
Cost3SVM = ifelse(predict(radial.cost3.svm.fit) > 0, 1, 0),
Cost4SVM = ifelse(predict(radial.cost4.svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c(‘X’, ‘Y’))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)
Zmiany wywołane parametrem kosztu są dość subtelne, ale można je zobaczyć na obrzeżach zestawu danych pokazanego poniżej. W miarę wzrostu kosztów granice tworzone przez jądro radialne stają się coraz bardziej liniowe
Po przeanalizowaniu parametru kosztu zakończymy nasze eksperymenty z hiperparametrami SVM, grając z hiperparametrem gamma. Do celów testowych obserwujemy jego wpływ na jądro sigmoidalne, testując cztery różne wartości gamma:
sigmoid.gamma1.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘sigmoid’,
gamma = 1)
with(df, mean(Label == ifelse(predict(sigmoid.gamma1.svm.fit) > 0, 1, 0)))
#[1] 0.478
sigmoid.gamma2.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘sigmoid’,
gamma = 2)
with(df, mean(Label == ifelse(predict(sigmoid.gamma2.svm.fit) > 0, 1, 0)))
#[1] 0.4824
sigmoid.gamma3.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘sigmoid’,
gamma = 3)
with(df, mean(Label == ifelse(predict(sigmoid.gamma3.svm.fit) > 0, 1, 0)))
#[1] 0.4816
sigmoid.gamma4.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = ‘sigmoid’,
gamma = 4)
with(df, mean(Label == ifelse(predict(sigmoid.gamma4.svm.fit) > 0, 1, 0)))
#[1] 0.4824
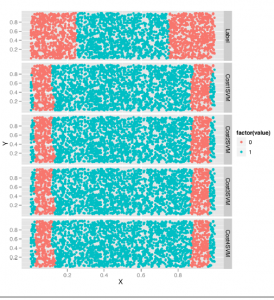
Za każdym razem, gdy zwiększamy gamma, model robi się trochę lepiej. Aby znaleźć źródło tego ulepszenia, przejdźmy do graficznej diagnostyki prognoz:
df <- df[, c(‘X’, ‘Y’, ‘Label’)]
df <- cbind(df,
data.frame(Gamma1SVM = ifelse(predict(sigmoid.gamma1.svm.fit) > 0, 1, 0),
Gamma2SVM = ifelse(predict(sigmoid.gamma2.svm.fit) > 0, 1, 0),
Gamma3SVM = ifelse(predict(sigmoid.gamma3.svm.fit) > 0, 1, 0),
Gamma4SVM = ifelse(predict(sigmoid.gamma4.svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c(‘X’, ‘Y’))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)
Jak widać, dość skomplikowana granica decyzyjna wybrana przez jądro sigmoidalne wypacza się, gdy zmieniamy wartość gamma.
Aby naprawdę uzyskać lepszą intuicję w tym, co się dzieje, zalecamy eksperymentowanie z dużo większą liczbą wartości gamma niż cztery, które przed chwilą pokazaliśmy. To kończy nasze wprowadzenie do SVM. Uważamy, że jest to cenny algorytm w twoim zestawi narzędzi, ale nadszedł czas, aby przestać budować zestaw narzędzi i zamiast tego zacząć skupiać się na krytycznym zastanowieniu się, które narzędzie jest najlepsze dla danego zadania. W tym celu zbadamy wiele modeli jednocześnie na jednym zestawie danych.