Naszym pierwszym krokiem w procesie analitycznym jest wyodrębnienie podstawowych elementów wykresu. Istnieją dwa przydatne podgrupy pełnego obiektu user.net, które będziemy chcieli wyodrębnić. Najpierw przeprowadzimy analizę k-core, aby wyodrębnić 2-rdzeniowy wykresu. Z definicji analiza k-core rozkłada wykres według połączeń węzłów. Aby znaleźć „rdzeń” wykresu, chcemy wiedzieć, ile węzłów ma określony stopień. Rdzeń k opisuje stopień rozkładu. Tak więc dwurdzeniowy wykres jest podgrafem węzłów, które mają stopień dwa lub więcej. Jesteśmy zainteresowani wydobyciem 2-rdzeniowego, ponieważ naturalnym produktem ubocznym wyszukiwania kuli śnieżnej jest posiadanie wielu wiszących węzłów na zewnątrz sieci. Te wisiorki wnoszą bardzo niewiele, jeśli w ogóle, użytecznych informacji o strukturze sieci, dlatego chcemy je usunąć. Pamiętaj jednak, że wykres Twittera jest skierowany, co oznacza, że węzły mają stopień wejściowy i wyjściowy. Aby znaleźć te węzły, które są bardziej odpowiednie dla tej analizy, użyjemy funkcji graph.coreness do obliczenia rdzenia każdego węzła według jego in-stop poprzez ustawienie parametru mode = „in”. Robimy to, ponieważ chcemy zachować te węzły, które otrzymują co najmniej dwie krawędzie, a nie te, które dają dwie krawędzie. Te wisiorki zmiecione w próbce śnieżki prawdopodobnie będą miały połączenie z siecią, ale nie z niej; dlatego używamy stopnia, aby je znaleźć.
user.cores <- graph.coreness (user.net, mode = “in”)
user.clean <- subgraph (user.net, który (user.cores> 1) -1)
Funkcja podgrafu przyjmuje jako dane wejściowe obiekt wykresu i zestaw węzłów i zwraca podgraf wywołany przez te węzły na przekazanym wykresie. Aby wyodrębnić 2-rdzeniowy wykres z user.net, używamy podstawy R, która działa w celu znalezienia tych węzłów o współczynniku rdzenia większym niż jeden.
user.ego <- subgraph (user.net, c (0neighbors (user.net, user, mode = “out”)))
Jednym z najbardziej frustrujących „problemów” związanych z pracą z igraphem jest to ,że igraph używa indeksowania zerowego dla węzłów, podczas gdy R rozpoczyna indeksowanie od jednego. W 2-rdzeniowym przykładzie zauważysz, że odejmujemy jeden z wektora zwracanego przez funkcję what, abyśmy nie napotkali przerażającego błędu „off by one”. Drugi kluczowy podgraf, który wyodrębnimy, to sieć ego nasion. Przypomnij sobie, że jest to wykres podrzędny wywołany przez sąsiadów nasion. Na szczęście igraph ma przydatną funkcję wygody sąsiadów do identyfikacji tych węzłów. Znów jednak musimy być świadomi struktury grafów ukierunkowanych na Twitterze. Sąsiedzi węzła mogą być albo wychodzący, więc musimy powiedzieć funkcji sąsiadów, którą chcielibyśmy. W tym przykładzie zbadamy sieć ego wywołaną przez zewnętrznych sąsiadów lub użytkowników Twittera, za którymi podąża ziarno, a nie tych, którzy podążają za ziarnem. Z analitycznego punktu widzenia bardziej interesujące może być zbadanie użytkowników, których ktoś obserwuje, szczególnie jeśli badasz własne dane. To powiedziawszy, alternatywa może być również interesująca i zachęcamy czytelnika do ponownego uruchomienia tego kodu i spojrzenia na niezależnych sąsiadów. Przez resztę tego rozdziału skupimy się na sieci ego, ale 2-rdzeniowy jest bardzo przydatny do innych analiz sieciowych, więc zapiszemy go w ramach pobierania danych. Teraz jesteśmy gotowi przeanalizować sieć ego, aby znaleźć strukturę lokalnej społeczności. W tym ćwiczeniu będziemy używać jednej z najbardziej podstawowych metod określania członkostwo w społeczności: hierarchiczne grupowanie odległości między węzłami. To kęs, ale koncepcja jest dość prosta. Zakładamy, że węzły, w tym przypadku użytkownicy Twittera, którzy są bliżej połączeni, tj. mają mniej przeskoków między sobą, są bardziej podobni. Ma to sens praktycznie, ponieważ możemy uważać, że osoby o wspólnych zainteresowaniach śledzą się na Twitterze, a zatem mają mniejsze odległości między nimi. Interesujące jest to, jak wygląda ta struktura społeczności dla danego użytkownika, ponieważ ludzie mogą mieć kilka różnych społeczności w swojej sieci ego.
user.sp <- shortest.paths (user.ego)
user.hc <- hclust (dist (user.sp))
Pierwszym krokiem w przeprowadzeniu takiej analizy jest pomiar odległości między wszystkimi węzłami na naszym wykresie. Używamy shortest.paths, która zwraca macierz N na N, gdzie N jest liczbą węzłów na wykresie, a najkrótsza odległość między każdą parą węzłów jest wpisem dla każdej pozycji w macierzy. Wykorzystamy te odległości do obliczenia partycji węzłów na podstawie odległości między nimi. Jak sama nazwa wskazuje, klastrowanie „hierarchiczne” ma wiele poziomów. Proces tworzy te poziomy lub cięcia, próbując utrzymać najbliższe węzły w tych samych partycjach, gdy rośnie liczba partycji. Dla każdej warstwy w dalszej części hierarchii zwiększamy liczbę partycji lub grup węzłów o jeden. Za pomocą tej metody możemy iteracyjnie rozkładać graf na bardziej szczegółowe grupy węzłów, zaczynając od wszystkich węzłów w tej samej grupie i przechodząc w dół hierarchii, aż wszystkie węzły znajdą się w swojej grupie.
R zawiera wiele przydatnych funkcji do tworzenia klastrów. W tej pracy użyjemy kombinacji funkcji dist i hclust. Funkcja dist utworzy macierz odległości z macierzy obserwacji. W naszym przypadku obliczyliśmy już odległości za pomocą funkcji shortest.path, więc funkcja dist służy do konwersji tej macierzy w coś, z czym może współpracować hclust. Funkcja hclust wykonuje klastrowanie i zwraca specjalny obiekt, który zawiera wszystkie potrzebne informacje o klastrowaniu. Jedną przydatną rzeczą do zrobienia po klastrowaniu czegoś hierarchicznie jest przeglądanie dendrogramu partycji. Dendrogram tworzy diagram podobny do drzewa, który pokazuje, w jaki sposób klastry rozdzielają się podczas przechodzenia dalej w dół hierarchii. To da nam pierwszy wgląd w strukturę społeczności naszej sieci ego. Jako przykład przyjrzyjmy się dendrogramowi ego-sieci Johna na Twitterze, który jest zawarty w katalogu danych / tego rozdziału. Aby wyświetlić jego dendrogram, załadujemy jego dane ego-network, przeprowadzimy grupowanie, a następnie przekażemy obiekt hclust do funkcji wydruku, która wie, jak narysować dendrogram.
user.ego <- read.graph(‘data/johnmyleswhite/johnmyleswhite_ego.graphml’, format = ‘graphml’)
user.sp <- shortest.paths(user.ego)
user.hc <- hclust(dist(user.sp))
plot(user.hc)
Patrząc na rysunek
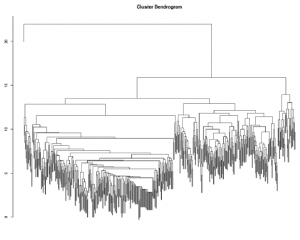
widzimy już naprawdę interesującą strukturę społeczności wyłaniającą się z sieci Twittera Johna. Wydaje się, że istnieje względnie czysty podział między dwiema społecznościami wysokiego poziomu, a następnie w obrębie tych jest wiele mniejszych, ściśle powiązanych podgrup. Oczywiście, dane wszystkich będą różne, a liczba społeczności, które zobaczysz, będzie w dużej mierze zależna od wielkości i gęstości twojej ego-sieci na Twitterze. Chociaż z naukowego punktu widzenia interesująca jest kontrola klastrów za pomocą dendrogramu, naprawdę chcielibyśmy zobaczyć je w sieci. Aby to zrobić, będziemy musieli dodać dane partycji lustering do węzłów, co zrobimy za pomocą prostej pętli, aby dodać pierwsze 10 nietrywialnych partycji do naszej sieci. Przez nietrywialne rozumiemy, że pomijamy pierwszą partycję, ponieważ partycja ta przypisuje wszystkie węzły do tej samej grupy. Chociaż jest to ważne z punktu widzenia ogólnej hierarchii, nie daje nam żadnej struktury społeczności lokalnej.
for(i in 2:10) {
user.cluster <- as.character(cutree(user.hc, k=i))
user.cluster[1] <- “0”
user.ego <- set.vertex.attribute(user.ego, name=paste(“HC”,i,sep=””),
value=user.cluster)
}
Funkcja cutree zwraca przypisanie partycji dla każdego elementu w hierarchii na danym poziomie, tzn. „Wycina drzewo”. Algorytm klastrowania nie wie, że daliśmy mu sieć ego, w której pojedynczy węzeł jest punktem centralnym, więc zgrupował nasze ziarno z innymi węzłami na każdym poziomie klastrowania. Aby ułatwić identyfikację użytkownika początkowego podczas wizualizacji, przypisujemy go do własnego klastra: „0”. Na koniec ponownie używamy funkcji set.vertex.attributes, aby dodać te informacje do naszego obiektu wykresu. Mamy teraz obiekt wykresu zawierający nazwy Twittera i pierwszych 10 partycji klastrowych z naszej analizy. Zanim będziemy mogli uruchomić Gephi i wizualizować wyniki, musimy zapisać obiekt wykresu w pliku. Użyjemy funkcji write.graph, aby wyeksportować te dane jako pliki GraphML. GraphML jest jednym z wielu formatów plików sieciowych i jest oparty na XML. Jest to przydatne do naszych celów, ponieważ nasz obiekt wykresu zawiera wiele metadanych, takich jak etykiety węzłów i partycje klastra. Podobnie jak w przypadku większości formatów opartych na XML, pliki GraphML mogą szybko się powiększać i nie są idealne do przechowywania danych relacyjnych
write.graph(user.net, paste(“data/”, user, “/”, user, “_net.graphml”, sep=””),
format=”graphml”)
write.graph(user.clean, paste(“data/”, user, “/”, user, “_clean.graphml”, sep=””),
format=”graphml”)
write.graph(user.ego, paste(“data/”, user, “/”, user, “_ego.graphml”, sep=””),
format=”graphml”)
Zapisujemy wszystkie trzy obiekty wykresów wygenerowane podczas tego procesu. W następnej części wizualizujemy te wyniki za pomocą Gephi, korzystając z przykładowych danych