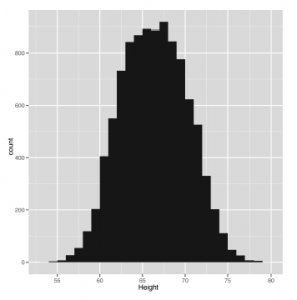
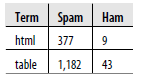
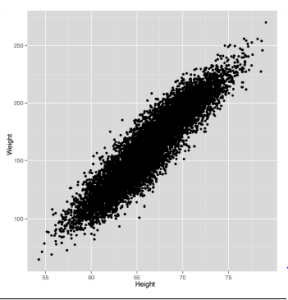
Obliczanie numerycznych podsumowań danych jest oczywiście cenne. W końcu to klasyczna statystyka. Ale dla wielu osób liczby nie przekazują informacji, które chcą zobaczyć bardzo skutecznie. Wizualizacja danych jest często bardziej skutecznym sposobem na wykrycie w nich wzorców. W tej sekcji omówimy dwie najprostsze formy wizualizacji danych eksploracyjnych: wizualizacje jednokolumnowe, które podkreślają kształt twoich danych, oraz wizualizacje dwukolumnowe, które podkreślają związek między parami kolumn. Oprócz pokazania narzędzi do wizualizacji danych, opiszemy również niektóre kanoniczne kształty, których możesz się spodziewać, gdy zaczniesz przeglądać dane. Te wyidealizowane kształty, zwane także rozkładami, są standardowymi wzorami, które statystycy badali przez lata. Gdy znajdziesz jeden z tych kształtów w swoich danych, często możesz wyciągać szerokie wnioski na temat swoich danych: jak powstało, jakie abstrakcyjne właściwości będzie miał, i tak dalej. Nawet jeśli uważasz, że kształt, który widzisz, jest tylko niejasnym przybliżeniem twoich danych, standardowe kształty dystrybucyjne mogą dostarczyć bloków konstrukcyjnych, których możesz użyć do zbudowania bardziej złożonych kształtów, które bardziej pasują do twoich danych. To powiedziawszy, zacznijmy od wizualizacji danych o wysokościach i wagach, z którymi pracowaliśmy do tej pory. W rzeczywistości jest to dość złożony zestaw danych, który ilustruje wiele pomysłów, które będziemy napotykać wielokrotnie w tym tekście. Najbardziej typową techniką wizualizacji z jedną kolumną, z której korzystają ludzie, jest histogram. Na histogramie dzielisz zestaw danych na pojemniki, a następnie zliczasz liczbę wpisów w danych, które mieszczą się w każdym z pojemników. Na przykład na rysunku tworzymy histogram z jednocalowymi przedziałami, aby wizualizować nasze dane dotyczące wysokości.
Możemy to zrobić w R w następujący sposób:
library(„ggplot2”)
data.file <- file.path („data”, „01_heights_weights_genders.csv”)
heights.weights <- read.csv (data.file, header = TRUE, sep = ‘,’)
ggplot (heights.weights, aes (x = Height)) + geom_histogram (binwidth = 1)
Natychmiast coś powinno na ciebie wyskoczyć: w twoich danych jest kształt krzywej dzwonowej. Większość wpisów znajduje się w środku danych, blisko średniej i mediany wysokości. Istnieje jednak niebezpieczeństwo, że ten kształt jest iluzją spowodowaną przez rodzaj używanego histogramu. Jednym ze sposobów sprawdzenia tego jest próba użycia kilku innych przepustowości. To jest coś o czym. pracując z histogramami, zawsze powinieneś o tym pamiętać: stosowane przez Ciebie szerokości bin nakładają na twoją dane zewnętrzną strukturę, jednocześnie ujawniając wewnętrzną strukturę twoich danych. Znalezione wzory, nawet jeśli są prawdziwe, mogą bardzo łatwo zniknąć, jeśli użyjesz niewłaściwych ustawień do zbudowania histogramu. Poniżej odtwarzamy histogram z użyciem pięciocalowych pojemników z następującym kodem R:
ggplot (heights.weights, aes (x = Height)) + geom_histogram (binwidth = 5)
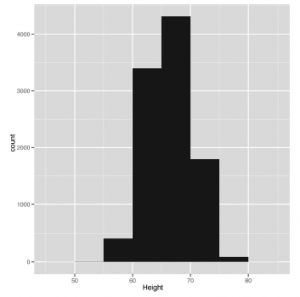
Gdy używamy zbyt szerokiego przedziału, duża część naszych danych zanika. Nadal jest szczyt, ale symetria, którą widzieliśmy wcześniej, wydaje się w większości zanikać. Nazywa się to wygładzaniem. I odwrotny problem, zwany niedopasowaniem, jest równie niebezpieczny. Na rysunku ponownie dostosowujemy szerokość przedziału, tym razem do znacznie mniejszych 0,001 cali:
ggplot (heights.weights, aes (x = Height)) + geom_histogram (binwidth = 0,001)
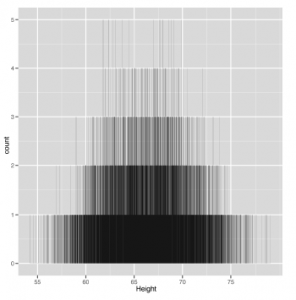
W tym przypadku nie osiągnęliśmy wygładzenia danych, ponieważ użyliśmy niewiarygodnie małych pojemników. Ponieważ mamy tyle danych, nadal możesz nauczyć się czegoś z tego histogramu, ale zestaw danych ze 100 punktami byłby w zasadzie bezwartościowy, gdybyś użył tego rodzaju powiązania. Ponieważ ustawianie wiązań może być żmudne i ponieważ nawet najlepszy histogram jest zbyt postrzępiony dla naszego gustu, preferujemy alternatywę dla histogramów zwanych szacunkami gęstości jądra (KDE) lub wykresami gęstości. Chociaż wykresy gęstości cierpią z powodu większości tych samych problemów z nadmiernym wygładzaniem i wygładzaniem, które występują w histogramach, generalnie uważamy je za lepsze pod względem estetycznym – szczególnie dlatego, że wykresy gęstości dla dużych zestawów danych przypominają bardziej kształty teoretyczne, których spodziewamy się w naszych danych. Ponadto wykresy gęstości mają pewną przewagę teoretyczną nad histogramami: teoretycznie użycie wykresu gęstości powinno wymagać mniejszej liczby punktów danych, aby ujawnić podstawowy kształt danych niż histogram. Na szczęście wykresy gęstości są tak samo łatwe do wygenerowania w R jak histogramy. Na rysunku tworzymy nasz pierwszy wykres gęstości danych wysokości:
ggplot (heights.weights, aes (x = Height)) + geom_density ()
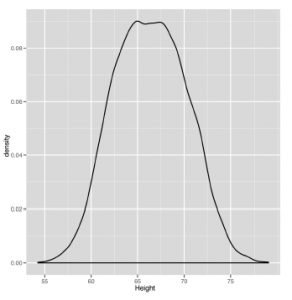
Gładkość wykresu gęstości pomaga nam odkryć rodzaje wzorów, które osobiście uważamy za trudniejsze do zobaczenia na histogramach. Tutaj wykres gęstości sugeruje, że dane są podejrzanie płaskie przy wartości szczytowej. Ponieważ standardowy kształt krzywej dzwonowej, którego moglibyśmy się spodziewać, nie jest płaski, prowadzi nas to do zastanowienia się, czy w tym zbiorze danych nie kryje się więcej struktur. Jedną rzeczą, którą możesz spróbować zrobić, gdy uważasz, że brakuje Ci struktury, jest podzielenie wykresu na dowolne dostępne zmienne jakościowe. Tutaj używamy płci każdego punktu, aby podzielić nasze dane na dwie części. Następnie na rysunku poniżej tworzymy wykres gęstości, w którym nałożone są dwie gęstości, ale są one ubarwione inaczej, aby wskazać reprezentowaną przez nich płeć:
ggplot (heights.weights, aes (x = Height, fill = Gender)) + geom_density ()
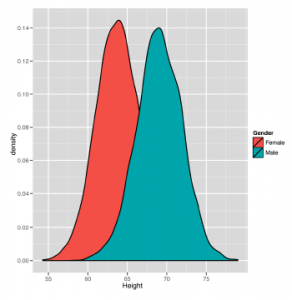
Na tym wykresie nagle widzimy ukryty wzór, którego wcześniej całkowicie brakowało: nie patrzymy na jedną krzywą dzwonkową ale na dwie różne krzywe dzwonka, które częściowo się pokrywają. Nie jest to zaskakujące, ponieważ kobiety i mężczyźni mają różne średnie wysokości. Możemy spodziewać się tej samej struktury krzywej dzwonowej we wzorach dla obu płci. Poniżej tworzymy nowy wykres gęstości dla kolumny wag naszego zestawu danych:
ggplot (heights.weights, aes (x = Weight, fill = Gender)) + geom_density ()
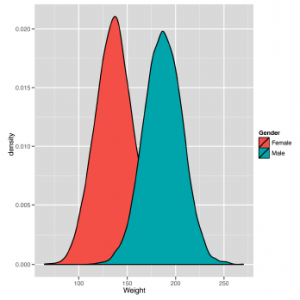
Ponownie widzimy tę samą mieszaninę krzywych dzwonowych w strukturze. W przyszłych sekcjach omówimy bardziej szczegółowo tę mieszankę krzywych dzwonowych, ale warto nadać nazwę strukturze, na którą patrzymy teraz: jest to model mieszany, w którym dwie standardowe rozkłady zostały zmieszane, aby uzyskać dystrybucję niestandardową. Oczywiście musimy jaśniej opisać nasze standardowe rozkłady, aby nadać sens temu zdaniu, więc zacznijmy od naszego pierwszego wyidealizowanego rozkładu danych: rozkładu normalnego, który jest również nazywany rozkładem Gaussa lub krzywą dzwonową. Możemy łatwo zobaczyć przykład normalnego rozkładu, po prostu dzieląc wykres na dwie części, zwane fasetami. Robimy to poniżej z wykresami gęstości, które pokazaliśmy do tej pory, abyś mógł zobaczyć dwie krzywe dzwonowe w oderwaniu od siebie.
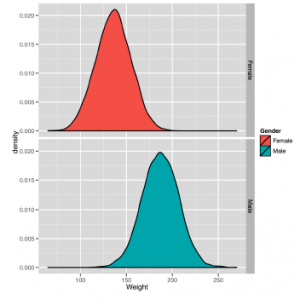
W R możemy zbudować tego rodzaju fasetowany wykres w następujący sposób:
ggplot (heights.weights, aes (x = Weight, fill = Gender)) + geom_density () + facet_grid (Gender ~.)
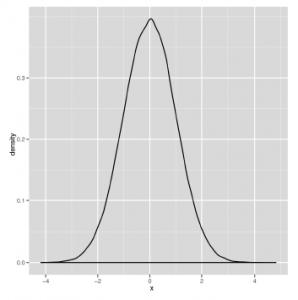
Gdy to zrobimy, wyraźnie widzimy jedną krzywą dzwonka wyśrodkowaną na 64 ”dla kobiet i inną krzywą dzwonkową wyśrodkowaną na 69” dla mężczyzn. Ta specyficzna krzywa dzwonowa jest rozkładem normalnym, kształtem, który pojawia się tak często, że łatwo jest myśleć, że jest to „normalny” sposób wyświetlania danych. To nie do końca prawda: wiele rzeczy, na których nam zależy, od rocznych dochodów ludzi po codzienne zmiany cen akcji, nie są bardzo dobrze opisane przy użyciu normalnej dystrybucji. Ale rozkład normalny jest bardzo ważny w matematycznej teorii statystyki, więc jest znacznie lepiej rozumiany niż większość innych rozkładów. Na bardziej abstrakcyjnym poziomie rozkład normalny jest tylko rodzajem krzywej dzwonowej. Może to być dowolna z krzywych dzwonka pokazanych na poniższych rysunkach
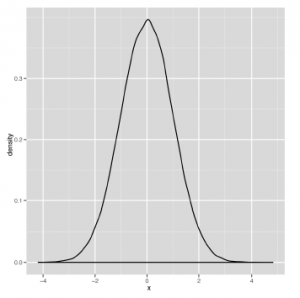
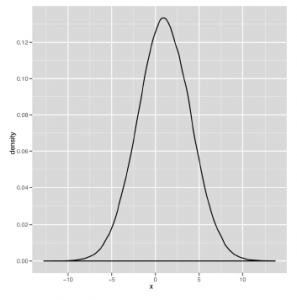
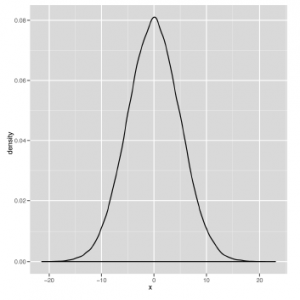
Na tych wykresach różnią się dwa parametry: średnia rozkładu, która określa środek krzywej dzwonowej i wariancja rozkładu, która określa szerokość krzywej dzwonowej. Powinieneś bawić się z wizualizacją różnych wersji krzywej dzwonowej, grając z parametrami w poniższym kodzie, aż poczujesz się komfortowo z wyglądem krzywej dzwonowej. Aby to zrobić, graj z wartościami m i s w kodzie pokazanym tutaj:
m <- 0
s <- 1
ggplot (data.frame (X = rnorm (100000, m, s)), aes (x = X)) + geom_density ()
Wszystkie krzywe, które można wygenerować za pomocą tego kodu, mają ten sam podstawowy kształt; zmiana m i s jedynie przesuwa środek i kurczy się lub powiększa szerokość. Jak widać na powyższych rysunkach, dokładny kształt krzywych będzie się różnił, ale ich ogólny kształt jest spójny. Niestety, zobaczenie tego ogólnego kształtu dzwonu nie wystarczy, aby powiedzieć, że Twoje dane są normalne, ponieważ istnieją inne rozkłady w kształcie dzwonu, z których jeden opiszemy za chwilę. Na razie zróbmy krótką lekcję żargonu, ponieważ normalny rozkład pozwala nam zdefiniować kilka jakościowych pomysłów na temat kształtu danych. Najpierw wróćmy do tematu trybów, które odkładaliśmy do tej pory. Jak powiedzieliśmy wcześniej, tryb ciągłej listy liczb nie jest dobrze zdefiniowany, ponieważ żadne liczby się nie powtarzają. Ale tryb ma czytelną interpretację wizualną: kiedy tworzysz wykres gęstości, trybem danych jest szczyt dzwonu. Na przykład spójrz na rysunek
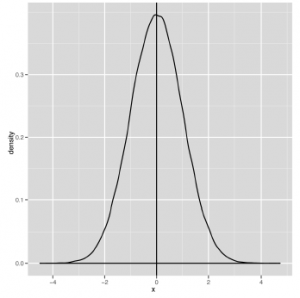
Oszacowanie trybów wizualnych jest znacznie łatwiejsze w przypadku wykresu gęstości niż w przypadku histogramu, co jest jednym z powodów, dla których wolimy wykresy gęstości niż histogramy. A tryby mają sens niemal natychmiast, gdy patrzysz na wykresy gęstości, podczas gdy często mają one bardzo niewielki sens, jeśli próbujesz pracować bezpośrednio z liczbami. Teraz, gdy zdefiniowaliśmy tryb, powinniśmy wskazać, że jedną z cech definiujących rozkład normalny jest to, że ma on pojedynczy tryb, który jest również średnią i medianą danych, które opisuje . Natomiast wykres podobny do pokazanego tu
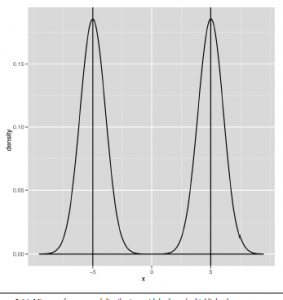 ,
,
ma dwa tryby, a wykres
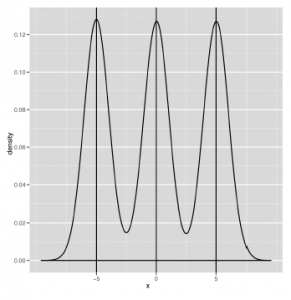
ma trzy tryby. Kiedy mówimy o liczbie trybów, które widzimy w naszych danych, użyjemy następujących terminów: rozkład z jednym trybem jest jednomodalny, rozkład z dwoma trybami jest bimodalny, a rozkład z dwoma lub więcej trybami jest multimodalny. Kolejne ważne jakościowe rozróżnienie można wprowadzić między danymi symetrycznymi a danymi wypaczonymi. Rysunki
i
pokazują obrazy danych symetrycznych i przekrzywionych, aby wyjaśnić te terminy. Rozkład symetryczny ma ten sam kształt, niezależnie od tego, czy przesuniesz się na lewo od trybu, czy na prawo od trybu. Rozkład normalny ma tę właściwość, która mówi nam, że równie dobrze możemy zobaczyć dane znajdujące się poniżej trybu, jak i dane powyżej tego trybu. Natomiast drugi wykres, zwany rozkładem gamma, jest przekrzywiony w prawo, co oznacza, że znacznie bardziej prawdopodobne jest zobaczenie skrajnych wartości po prawej stronie trybu niż skrajnych wartości po lewej stronie tryb. Ostatnie jakościowe rozróżnienie, które wprowadzimy, to między danymi cienkościennymi a danymi gruboziarnistymi. W sekundę pokażemy standardowy wykres, który ma zilustrować to rozróżnienie, ale to rozróżnienie jest prawdopodobnie łatwiejsze do sformułowania. Cienkoziarnisty rozkład zwykle daje wartości, które nie są daleko od średniej; powiedzmy, że robi to w 99% przypadków. Na przykład rozkład normalny daje wartości, które są nie większe niż trzy standardowe odchylenia od średniej w około 99% przypadków. Natomiast inny rozkład w kształcie dzwonu zwany rozkładem Cauchy’ego wytwarza tylko 90% jego wartości w tych trzech granicach odchylenia standardowego. I w miarę oddalania się od wartości średniej, dwa typy rozkładów stają się jeszcze bardziej różne: rozkład normalny prawie nigdy nie wytwarza wartości, które są o sześć standardowych odchyleń od średniej, podczas gdy Cauchy zrobi to prawie 5% czas. Kanoniczne obrazy, które są zwykle używane do wyjaśnienia tego rozróżnienia między cienkim normalnym a grubym Cauchy, pokazano na rysunkach
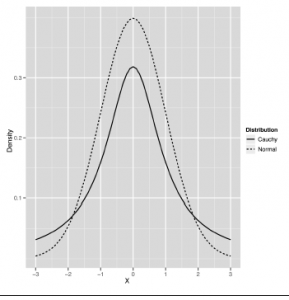
i
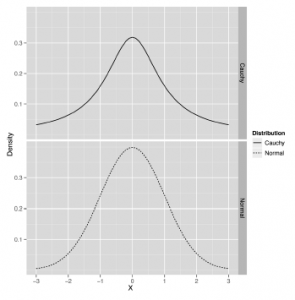
Uważamy jednak, że dzięki intuicyjnemu generowaniu dużej ilości danych z obu tych dystrybucji uzyskasz bardziej intuicyjne zrozumienie i zobaczysz wyniki dla siebie. R sprawia, że jest to dość łatwe, dlatego powinieneś spróbować:
set.seed(1)
normal.values <- rnorm(250, 0, 1)
cauchy.values <- rcauchy(250, 0, 1)
range(normal.values)
range(cauchy.values)
Wykreślenie ich sprawi, że kwestia będzie bardziej zrozumiała:
ggplot (data.frame (X = normal.values), aes (x = X)) + geom_density ()
ggplot (data.frame (X = wartości cauchy.)), aes (x = X)) + geom_density ()
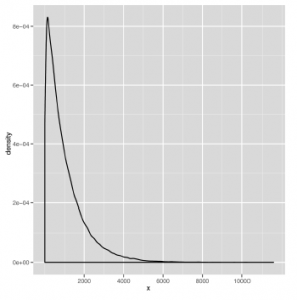
Aby zakończyć tą część o rozkładzie normalnym i jego kuzynce rozkładzie Cauchy’ego, jeszcze raz podsumujmy jakościowe właściwości normalnego: jest on jednomodalny, symetryczny i ma kształt dzwonu z cienkimi ogonami. Cauchy jest unimodalny i symetryczny, i ma kształt dzwonu z ciężkimi ogonami. Po rozkładzie normalnym są jeszcze dwa obrazy kanoniczne, które chcemy wam pokazać, zanim zamkniemy tę sekcję na wykresach gęstości: łagodnie przekrzywiony rozkład zwany gamma i bardzo przekrzywiony rozkład zwany wykładniczym. Wykorzystamy oba później, ponieważ występują one w rzeczywistych danych, ale warto je teraz opisać, aby zilustrować skośność wizualnie. Zacznijmy od rozkładu gamma.
gamma .values<- rgamma (100000, 1, 0,001)
ggplot (data.frame (X = wartości gamma), aes (x = X)) + geom_density ()
Wynikowy wykres danych gamma pokazano tu
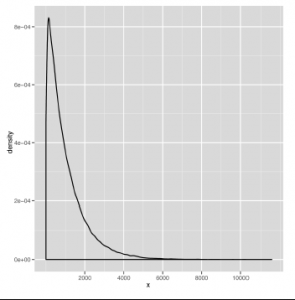
Jak widać, rozkład gamma jest przekrzywiony w prawo, co oznacza, że mediana i średnia mogą czasami być zupełnie inne. Na rysunku
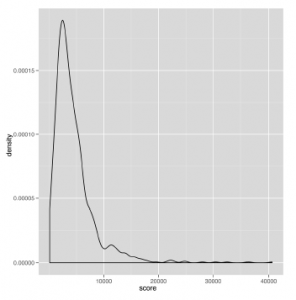
pokazaliśmy wyniki niektórych osób, które graliśmy w grę Canabalt na iPhone’a. Ten prawdziwy zestaw danych wygląda niezwykle podobnie do danych, które mogłyby zostać wygenerowane przez teorię rozkładu gamma. Założymy się również, że zobaczysz tego rodzaju kształt na wykresach gęstości dla wyników w wielu innych grach, więc wydaje się, że jest to szczególnie przydatne narzędzie teoretyczne, które masz na swoim pasku, jeśli chcesz analizować dane gry.
Inną rzeczą, o której należy pamiętać, jest to, że rozkład gamma daje tylko wartości dodatnie. Kiedy opiszemy, jak używać stochastycznych narzędzi optymalizacyjnych pod koniec i, bardzo pozytywna dystrybucja będzie bardzo przydatna. Ostatnim rozkładem, który opiszemy, jest rozkład wykładniczy, który jest dobrym przykładem silnie wypaczonego rozkładu. Przykładowy zestaw danych zaczerpnięty z rozkładu wykładniczego pokazano na rysunku
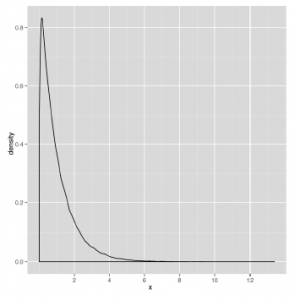
Ponieważ tryb rozkładu wykładniczego występuje przy wartości zerowej, jest prawie tak, jakbyś odciął dodatnią połowę dzwonu, aby utworzyć krzywą wykładniczą. Ten rozkład pojawia się dość często, gdy najczęstszą wartością w zbiorze danych jest zero i mogą wystąpić tylko wartości dodatnie. Na przykład korporacyjne centra telefoniczne często stwierdzają, że czas między otrzymywanymi połączeniami wygląda jak rozkład wykładniczy. Gdy zdobędziesz większą znajomość danych i dowiesz się więcej o teoretycznych rozkładach, które badali statystycy, te rozkłady będą ci bardziej znane – szczególnie dlatego, że te same nieliczne rozkłady pojawiają się w kółko. W tej chwili tak naprawdę zabierasz tę sekcję prostym terminom jakościowym, których możesz użyć, aby opisać swoje dane innym: jednomodalny kontra multimodalny, symetryczny kontra skośny i cienki lub gruby.
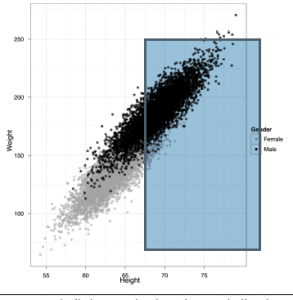
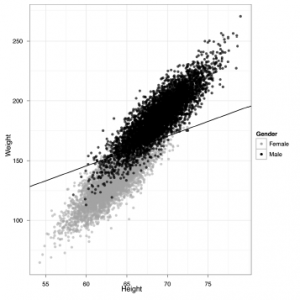











 ,
,






