Mówiliśmy o modelach zbyt złożonych, ale nigdy nie podaliśmy formalnej definicji złożoności. Jednym podejściem podczas pracy z regresją wielomianową byłoby stwierdzenie, że modele są bardziej złożone, gdy stopień jest większy; wielomian stopnia 2 jest na przykład bardziej złożony niż wielomian stopnia 1. Ale to ogólnie nie pomaga nam w regresji liniowej. Wykorzystamy więc alternatywną miarę złożoności: powiemy, że model jest skomplikowany, gdy współczynniki są duże. Na przykład powiedzielibyśmy, że model y ~ 5 * x + 2 jest bardziej skomplikowany niż model y ~ 3 * x + 2. Zgodnie z tą samą logiką powiemy, że model y ~ 1 * x ^ 2 + 1 * x + 1 jest bardziej skomplikowany niż model y ~ 1 * x + 1. Aby zastosować tę definicję w praktyce, możemy dopasować model za pomocą lm, a następnie zmierzyć jego złożoność poprzez zsumowanie wartości zwróconych przez cewkę:
lm.fit <- lm (y ~ x)
model.complexity <- sum (coef (lm.fit) ^ 2)
Tutaj wyliczyliśmy współczynniki przed ich zsumowaniem, aby nie wzajemnie się anulowały, gdy dodamy je wszystkie razem. Ten krok do kwadratu jest często nazywany normą L2. Alternatywnym podejściem do wyrównywania współczynników jest wzięcie zamiast tego bezwzględnej wartości współczynników; to drugie podejście nazywa się normą L1. Tutaj obliczamy dwa z nich w R:
lm.fit <- lm (y ~ x)
l2.model.complexity <- sum (coef (lm.fit) ^ 2)
l1.model.complexity <- sum (abs (coef (lm.fit)))
Te miary złożoności modelu mogą początkowo wydawać się dziwne, ale za chwilę przekonasz się, że naprawdę są pomocne, gdy próbujesz zapobiec nadmiernemu dopasowaniu. Powodem jest to, że możemy użyć tej miary złożoności, aby zmusić nasz model do uproszczenia podczas dopasowywania modelu. Wielki pomysł polega na tym, że kompromisowo dostosowujemy model tak, aby jak najlepiej pasował do danych treningowych, biorąc pod uwagę stopień złożoności modelu. To prowadzi nas do jednego z najbardziej krytycznych kryteriów decyzyjnych podczas modelowania danych: ponieważ dokonujemy kompromisu między dopasowaniem danych a złożonością modelu, ostatecznie wybieramy prostszy model, który pasuje gorzej, niż bardziej złożony model, który lepiej pasuje . Ten kompromis, który rozumiemy przez regularyzację, ostatecznie zapobiega nadmiernemu dopasowaniu, ograniczając naszemu modelowi dopasowanie hałasu w danych szkoleniowych, których używamy, aby go dopasować. Na razie porozmawiajmy o narzędziach, których możesz użyć do pracy z regularyzacją w R. W tym rozdziale zajmiemy się używaniem pakietu glmnet, który udostępnia funkcję o nazwie glmnet, która pasuje do modeli liniowych z wykorzystaniem regularyzacji. Aby zobaczyć, jak działa Glmnet, wróćmy jeszcze raz do naszych danych sinusoidalnych:
set.seed(1)
x <- seq(0, 1, by = 0.01)
y <- sin(2 * pi * x) + rnorm(length(x), 0, 0.1)
Aby użyć glmnet, musimy najpierw przekonwertować naszą wektorową kopię x na macierz za pomocą funkcji macierzy. Następnie wywołujemy glmnet w odwrotnej kolejności niż ta, której użyłbyś z lm i jego składnią ~ -operator:
x <- matrix(x)
library(‘glmnet’)
glmnet(x, y)
#Call: glmnet(x = x, y = y)
#
# Df %Dev Lambda
# [1,] 0 0.00000 0.542800
# [2,] 1 0.09991 0.494600
# [3,] 1 0.18290 0.450700
# [4,] 1 0.25170 0.410600
# [5,] 1 0.30890 0.374200
…
#[51,] 1 0.58840 0.005182
#[52,] 1 0.58840 0.004721
#[53,] 1 0.58850 0.004302
#[54,] 1 0.58850 0.003920
#[55,] 1 0.58850 0.003571
Kiedy wywołujesz glmnet w ten sposób, odzyskujesz cały zestaw możliwych regularyzacji regresji, o którą poprosiłeś ją. Na górze listy znajduje się najsilniejsza regularyzacja wykonana przez glmnet, a na dole listy jest najsłabsza obliczona normalizacja. W wynikach, które cytowaliśmy tutaj, pokazujemy pierwsze pięć wierszy i pięć ostatnich. Porozmawiajmy o interpretacji każdej kolumny wyniku dla tych 10 wierszy, które pokazaliśmy. Każdy wiersz wyniku zawiera trzy kolumny: (1) Df, (2)% Dev i (3) Lambda. Pierwsza kolumna, Df, mówi, ile współczynników w modelu skończyło się na niezerowych. Pamiętaj, że nie obejmuje to terminu przechwytywania, którego nie chcesz karać za jego rozmiar. Znajomość liczby niezerowych współczynników jest przydatna, ponieważ wiele osób chciałoby być w stanie stwierdzić, że tylko kilka danych wejściowych naprawdę ma znaczenie, i możemy to zapewnić bardziej pewnie, jeśli model działa dobrze, nawet gdy przypisuje zerową wagę wielu wejściom. Gdy większość danych wejściowych do modelu statystycznego ma przypisane zerowe współczynniki, mówimy, że model jest rzadki. Opracowywanie narzędzi do promowania rzadkości w modelach statystycznych jest głównym tematem we współczesnych badaniach nad uczeniem maszynowym. Druga kolumna,% Dev, jest zasadniczo R2 dla tego modelu. W górnym rzędzie wynosi 0%, ponieważ masz zerowy współczynnik dla jednej zmiennej wejściowej, a zatem nie możesz uzyskać lepszej wydajności niż zwykłe przechwytywanie. W dolnym rzędzie Dev wynosi 59%, co jest wartością, którą uzyskałbyś, używając lm bezpośrednio, ponieważ lm w ogóle nie dokonuje żadnej regularyzacji. Pomiędzy tymi dwiema skrajnościami regularyzacji modelu aż do przechwytywania i wcale nie regulowania, zobaczysz wartości dla Dev w zakresie od 9% do 58%. Ostatnia kolumna, Lambda, jest najważniejszą informacją dla kogoś, kto uczy się o regularyzacji. Lambda to parametr algorytmu regularyzacji, który kontroluje stopień złożoności dopasowanego modelu. Ponieważ kontroluje wartości, które ostatecznie uzyskasz dla głównych parametrów modelu, Lambda jest często nazywany hiperparametrem. Kiedy Lambda jest bardzo duża, bardzo karzesz swój model za to, że jest złożony, a ta penalizacja popycha wszystkie współczynniki w kierunku zera. Kiedy Lambda jest bardzo mała, wcale nie karasz za swój model. Na najdalszym końcu tego spektrum, w kierunku słabszej regularyzacji, możemy ustawić Lambdę na 0 i uzyskać wyniki takie jak te z nieregularnej regresji liniowej takiej, jaką pasowalibyśmy przy użyciu lm. Ale generalnie gdzieś w tych dwóch skrajnościach możemy znaleźć ustawienie dla Lambdy, które daje najlepszy możliwy model. Jak znaleźć tę wartość dla Lambda? Tutaj stosujemy walidację krzyżową jako część procesu pracy z regularyzacją. Zamiast bawić się stopniem regresji wielomianowej, możemy ustawić stopień na wysoką wartość, na przykład 10, już na początku. Następnie dopasujemy model z różnymi wartościami dla Lambda na zestawie treningowym i zobaczymy, jak działa na wyciągniętym zestawie testowym. Po zrobieniu tego dla wielu wartości Lambda, będziemy mogli zobaczyć, która wartość Lambda daje nam najlepszą wydajność na danych testowych. Absolutnie musisz ocenić jakość swojej regularyzacji na danych testowych. Zwiększenie siły regularyzacji może tylko pogorszyć Twoją wydajność w danych treningowych, więc dosłownie zero informacji możesz nauczyć się patrząc na swoją wydajność w danych treningowych. Mając to na uwadze, przejdźmy teraz do przykładu. Tak jak poprzednio, skonfigurujemy nasze dane i podzielimy je na zestaw szkoleniowy i testowy:
set.seed(1)
x <- seq(0, 1, by = 0.01)
y <- sin(2 * pi * x) + rnorm(length(x), 0, 0.1)
n <- length(x)
indices <- sort(sample(1:n, round(0.5 * n)))
training.x <- x[indices]
training.y <- y[indices]
test.x <- x[-indices]
test.y <- y[-indices]
df <- data.frame(X = x, Y = y)
training.df <- data.frame(X = training.x, Y = training.y)
test.df <- data.frame(X = test.x, Y = test.y)
rmse <- function(y, h)
{
return(sqrt(mean((y – h) ^ 2)))
}
Ale tym razem zapętlimy wartości Lambda zamiast stopni. Na szczęście nie musimy za każdym razem modernizować modelu, ponieważ glmnet przechowuje dopasowany model dla wielu wartości Lambda po jednym kroku dopasowania.
library(‘glmnet’)
glmnet.fit <- with(training.df, glmnet(poly(X, degree = 10), Y))
lambdas <- glmnet.fit$lambda
performance <- data.frame()
for (lambda in lambdas)
{
performance <- rbind(performance,
data.frame(Lambda = lambda,
RMSE = rmse(test.y, with(test.df, predict(glmnet.fit, poly(X,
degree = 10), s = lambda)))))
}
Po obliczeniu wydajności modelu dla różnych wartości Lambda, możemy skonstruować wykres, aby zobaczyć, gdzie w zakresie testowanych lambd możemy uzyskać najlepszą wydajność na nowych danych:
ggplot(performance, aes(x = Lambda, y = RMSE)) +
geom_point() +
geom_line()
Patrząc na rysunek ,
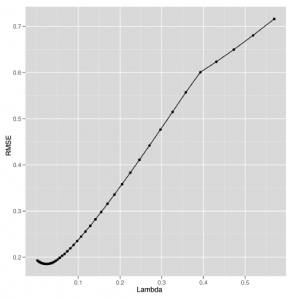
wygląda na to, że uzyskujemy najlepszą możliwą wydajność z Lambda blisko 0,05. Aby dopasować model do pełnych danych, możemy wybrać tę wartość i wyszkolić nasz model na całym zestawie danych. Tutaj robimy tylko to:
best.lambda <- with(performance, Lambda[which(RMSE == min(RMSE))])
glmnet.fit <- with(df, glmnet(poly(X, degree = 10), Y))
Po dopasowaniu naszego ostatecznego modelu do całego zestawu danych, możemy użyć coef do zbadania struktury naszego znormalizowanego modelu:
coef(glmnet.fit, s = best.lambda)
#11 x 1 sparse Matrix of class “dgCMatrix”
# 1
#(Intercept) 0.0101667
#1 -5.2132586
#2 0.0000000
#3 4.1759498
#4 0.0000000
#5 -0.4643476
#6 0.0000000
#7 0.0000000
#8 0.0000000
#9 0.0000000
#10 0.0000000
Jak widać z tej tabeli, ostatecznie używamy tylko 3 niezerowych współczynników, mimo że model ma możliwość użycia 10. Wybór prostszego modelu takiego, nawet jeśli możliwe są bardziej skomplikowane modele, jest główną strategią za regularyzacją. A dzięki regularyzacji w naszym zestawie narzędzi możemy w dużym stopniu zastosować regresję wielomianową i nadal powstrzymywać się od przeładowywania danych. Po wprowadzeniu podstawowych pomysłów na regularyzację, spójrzmy na praktyczne zastosowanie w studium przypadku