Zanim będziemy w stanie zapobiec nadmiernemu dopasowaniu, musimy nadać temu terminowi rygorystyczne znaczenie. Rozmawialiśmy o tym, że model jest nadmiernie dopasowany, gdy pasuje do części szumu w zestawie danych, a nie do prawdziwego podstawowego sygnału. Ale jeśli nie znamy prawdy, to jak możemy powiedzieć, że oddalamy się od niej, a nie bliżej? Sztuką jest wyjaśnienie, co rozumiemy przez prawdę. Dla naszych celów model predykcyjny jest bliski prawdy, gdy jego prognozy dotyczące przyszłych danych są dokładne. Ale oczywiście nie mamy dostępu do przyszłych danych; mamy tylko dane z przeszłości. Na szczęście możemy symulować, jak by to było mieć dostęp do danych w przyszłości, dzieląc nasze dane z przeszłości na dwie części. Prosty przykład wyjaśni naszą ogólną strategię: wyobraź sobie, że próbujemy zbudować model do przewidywania temperatur w przyszłości. Mamy dane za okres od stycznia do czerwca i chcemy dokonać prognoz na lipiec. Możemy sprawdzić, który z naszych modeli jest najlepszy, dopasowując je do danych od stycznia do maja, a następnie testując te modele na danych z czerwca. Gdybyśmy zrobili ten krok dopasowania modelu w maju, naprawdę testowalibyśmy nasz model na podstawie przyszłych danych. Możemy więc wykorzystać tę strategię dzielenia danych, aby wykonać całkowicie realistyczną symulację doświadczeń związanych z testowaniem naszego modelu na niewidzialnych danych. U podstaw weryfikacji krzyżowej leży po prostu nasza zdolność do symulowania testowania naszego modelu na przyszłych danych, ignorując część naszych danych historycznych podczas procesu dopasowania modelu. Jeśli przejrzałeś sprawy w rozdziałach 3 i 4, pamiętasz, że właśnie to zrobiliśmy. W każdym przypadku dzielimy nasze dane, aby trenować i testować nasze modele klasyfikacji i rankingu. Prawdopodobnie jest to po prostu instancja metody naukowej, której wszyscy uczono nas jako dzieci: (1) formułuje hipotezę, (2) zbiera dane i (3) ją testuje. Jest tylko odrobina sztuczki, ponieważ nie formułujemy hipotezy na podstawie istniejących danych, a następnie wychodzimy i zbieramy więcej danych. Zamiast tego ignorujemy część naszych danych podczas formułowania naszych hipotez, abyśmy mogli magicznie odkryć brakujące dane, gdy przyjdzie czas na przetestowanie naszych prognoz. Zanim skorzystamy z weryfikacji krzyżowej w złożonej aplikacji, przejrzyjmy zabawkowy przykład, w jaki sposób możemy użyć weryfikacji krzyżowej, aby wybrać stopień regresji wielomianowej dla danych fali sinusoidalnej, które mieliśmy wcześniej. Najpierw odtworzymy nasze dane fali sinusoidalnej:
set.seed(1)
x <- seq(0, 1, by = 0.01)
y <- sin(2 * pi * x) + rnorm(length(x), 0, 0.1)
Następnie musimy podzielić nasze dane na dwie części: zestaw szkoleniowy, którego użyjemy, aby dopasować do naszego modelu oraz zestaw testowy, którego użyjemy do przetestowania wydajności modelu. Zestaw treningowy można traktować jako dane z przeszłości, natomiast zestaw testowy to dane przyszłe. W tym przykładzie podzielimy dane dokładnie na pół. W przypadku niektórych aplikacji lepiej jest użyć więcej danych dla zestawu treningowego (powiedzmy, 80%) i mniej danych dla zestawu testowego (powiedzmy, 20%), ponieważ im więcej danych masz podczas dopasowywania modelu, tym lepiej dopasowany model będzie miał tendencję być. Jak zawsze twój przebieg będzie się różnił, więc eksperymentuj w obliczu jakiegokolwiek problemu w świecie rzeczywistym. Zróbmy podział, a następnie porozmawiajmy o szczegółach:
n <- length(x)
indices <- sort(sample(1:n, round(0.5 * n)))
training.x <- x[indices]
training.y <- y[indices]
test.x <- x[-indices]
test.y <- y[-indices]
training.df <- data.frame(X = training.x, Y = training.y)
test.df <- data.frame(X = test.x, Y = test.y)
Tutaj skonstruowaliśmy losowy wektor wskaźników, który definiuje zestaw treningowy. Dobrym pomysłem jest zawsze losowe dzielenie danych podczas dzielenia zestawu treningowego / zestawu testowego, ponieważ nie chcesz, aby zestaw treningowy i zestaw testowy systematycznie się różniły – tak może się zdarzyć, na przykład, jeśli wstawisz tylko najmniejsze wartości dla x do zestawu treningowego, a największe wartości do zestawu testowego. Losowość wynika z zastosowania funkcji próbki R, która generuje losową próbkę z danego wektora. W naszym przypadku podajemy wektor liczb całkowitych, od 1 do n, i próbkujemy ich połowę. Po ustaleniu wartości indeksów oddzielamy zestawy szkoleniowe i testowe, stosując reguły indeksowania wektorowego R. Na koniec tworzymy ramkę danych do przechowywania danych, ponieważ łatwiej jest pracować z lm podczas korzystania z ramek danych. Po podzieleniu danych na zestaw szkoleniowy i testowy chcemy przetestować różne stopnie pod kątem regresji wielomianowej, aby zobaczyć, która z nich działa najlepiej. Użyjemy RMSE do pomiaru naszej wydajności. Aby nasz kod był nieco czytelniejszy, stworzymy specjalną funkcję rmse:
rmse <- function(y, h)
{
return(sqrt(mean((y – h) ^ 2)))
}
Then we’ll loop over a set of polynomial degrees, which are the integers between
1 and 12:
performance <- data.frame()
for (d in 1:12)
{
poly.fit <- lm(Y ~ poly(X, degree = d), data = training.df)
performance <- rbind(performance,
data.frame(Degree = d,
Data = ‘Training’,
RMSE = rmse(training.y, predict(poly.fit))))
performance <- rbind(performance,
data.frame(Degree = d,
Data = ‘Test’,
RMSE = rmse(test.y, predict(poly.fit,
newdata = test.df))))
}
Podczas każdej iteracji tej pętli dopasowujemy regresję wielomianową stopnia d do danych w training.df, a następnie oceniamy jej wydajność zarówno na training.df, jak i test.df. Przechowujemy wyniki w ramce danych, abyśmy mogli szybko analizować wyniki po zakończeniu pętli. W tym przypadku używamy nieco innej techniki konstruowania ramek danych niż w przeszłości. Zaczynamy od przypisania pustej ramki danych zmiennej wydajności, do której następnie iteracyjnie dodajemy wiersze za pomocą funkcji rbind. Jak wspomnieliśmy wcześniej, często istnieje wiele sposobów wykonania tego samego zadania manipulacji danymi w języku R, ale rzadko pętla tego rodzaju jest najbardziej wydajna. Używamy go tutaj, ponieważ dane są dość małe i pozwala to na wyraźniejsze zrozumienie procesu algorytmu, ale pamiętaj o tym, pisząc własne testy wzajemnej weryfikacji. Po zakończeniu wykonywania pętli możemy wykreślić wydajność modeli regresji wielomianowej dla wszystkich stopni, których próbowaliśmy:
ggplot(performance, aes(x = Degree, y = RMSE, linetype = Data)) +
geom_point() +
geom_line()
Wynik pokazano poniżej
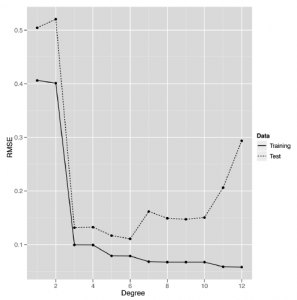
wyjaśnia, że użycie stopnia pośrodku zakresu, z którym eksperymentowaliśmy, zapewnia nam najlepszą wydajność naszych danych testowych. Gdy stopień jest tak niski jak 1 lub 2, model nie rejestruje prawdziwego wzorca w danych i widzimy bardzo słabą wydajność predykcyjną zarówno danych treningowych, jak i testowych. Gdy model nie jest wystarczająco skomplikowany, aby zmieścić nawet dane treningowe, nazywamy to niedopasowaniem. Na przeciwległym końcu naszego wykresu w pobliżu stopni 11 i 12 widzimy, że prognozy dla modelu znów zaczynają się pogarszać na danych testowych. Jest tak, ponieważ model staje się zbyt złożony i hałaśliwy, i pasuje do dziwactw w danych treningowych, których nie ma w danych testowych. Kiedy zaczynasz modelować dziwactwa losowe w swoich danych, nazywamy to nadmiernym dopasowaniem. Innym sposobem myślenia o nadmiernym dopasowaniu jest zauważenie, że nasza wydajność na zestawie treningowym i zestawie testowym zaczyna się różnić w miarę przesuwania się w prawo na powyższym rysunku: poziom błędu zestawu treningowego spada, ale wydajność zestawu testowego zaczyna rosnąć . Nasz model nie uogólnia na dane wykraczające poza określone punkty wyszkolonw na – i to sprawia, że się przepełnia. Na szczęście nasza fabuła informuje nas, jak ustawić stopień regresji, aby uzyskać najlepszą wydajność z naszego modelu. Ten punkt pośredni, który nie jest ani niedopasowany, ani nadmierny, byłby bardzo trudny do wykrycia bez zastosowania weryfikacji krzyżowej. Po krótkim objaśnieniu, w jaki sposób możemy zastosować walidację krzyżową w przypadku nadmiernego dopasowania, przejdziemy do omówienia innego podejścia do zapobiegania nadmiernemu dopasowaniu, które nazywa się regularyzacją. Normalizacja różni się znacznie od weryfikacji krzyżowej w duchu, nawet jeśli ostatecznie zastosujemy weryfikację krzyżową, aby pokazać, że regularyzacja jest w stanie zapobiec nadmiernemu dopasowaniu. Będziemy także musieli użyć weryfikacji krzyżowej, aby skalibrować nasz algorytm regularyzacji, więc te dwa pomysły ostatecznie zostaną ściśle powiązane.