Mając na uwadze nasze wcześniejsze zastrzeżenia, zacznijmy od regresji wielomianowej w R, która jest zaimplementowana w funkcji poly. Najłatwiejszym sposobem, aby zobaczyć, jak działa poly, jest zbudowanie z prostego przykładu i pokazanie, co się dzieje, gdy dajemy naszemu modelowi bardziej ekspresyjną moc naśladowania struktury naszych danych. Użyjemy fali sinusoidalnej, aby utworzyć zestaw danych, w którym związek między x i y nigdy nie może być opisany prostą linią.
set.seed(1)
x <- seq(0, 1, by = 0.01)
y <- sin(2 * pi * x) + rnorm(length(x), 0, 0.1)
df <- data.frame(X = x, Y = y)
ggplot(df, aes(x = X, y = Y)) +
geom_point()
Wystarczy spojrzeć na te dane, które pokazano na rysunku,
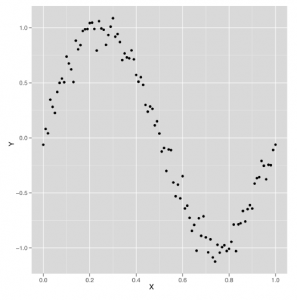
jasne jest, że użycie prostego modelu regresji liniowej nie zadziała. Ale uruchommy prosty model liniowy i zobaczmy, jak on działa.
summary(lm(Y ~ X, data = df))
#Call:
#lm(formula = Y ~ X, data = df)
#
#Residuals:
# Min 1Q Median 3Q Max
#-1.00376 -0.41253 -0.00409 0.40664 0.85874
#
#Coefficients:
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 0.94111 0.09057 10.39 <2e-16 ***
#X -1.86189 0.15648 -11.90 <2e-16 ***
#—
#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
#Residual standard error: 0.4585 on 99 degrees of freedom
#Multiple R-squared: 0.5885, Adjusted R-squared: 0.5843
#F-statistic: 141.6 on 1 and 99 DF, p-value: < 2.2e-16
Co zaskakujące, jesteśmy w stanie wyjaśnić 60% wariancji w tym zbiorze danych przy użyciu modelu liniowego – pomimo tego, że wiemy, że naiwny model regresji liniowej jest złym modelem danych falowych. Wiemy również, że dobry model powinien być w stanie wyjaśnić ponad 90% wariancji w tym zbiorze danych, ale nadal chcielibyśmy dowiedzieć się, co zrobił model liniowy, aby uzyskać tak dobre dopasowanie do danych. Aby odpowiedzieć na nasze pytanie, najlepiej wykreślić wyniki dopasowania regresji liniowej przy użyciu naszego preferowanego wariantu geom_smooth, w którym zmuszamy geom_smooth do użycia modelu liniowego, ustawiając metodę opcji = „lm”:
ggplot(data.frame(X = x, Y = y), aes(x = X, y = Y)) +
geom_point() +
geom_smooth(method = ‘lm’, se = FALSE)
Patrząc na rysunek
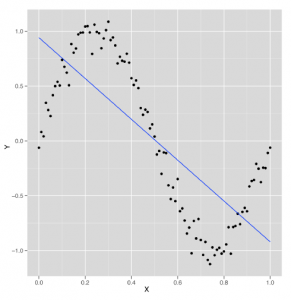
widzimy, że model liniowy znajduje sposób na uchwycenie połowy struktury fali sinusoidalnej za pomocą linii opadającej w dół. Ale to nie jest świetna strategia, ponieważ systematycznie lekceważysz te części danych, które nie są opisane przez tę nachyloną w dół linię. Jeśli fala sinusoidalna zostanie przedłużona o kolejny okres, R2 dla tego modelu nagle spadnie coraz bliżej 0%. Możemy wywnioskować, że domyślny model regresji liniowej przekracza dziwactwa naszego konkretnego zestawu danych i nie znajduje swojej prawdziwej podstawowej struktury falowej. Ale co, jeśli damy algorytmowi regresji liniowej więcej danych wejściowych do pracy? Czy znajdzie strukturę, która faktycznie jest falą? Jednym ze sposobów na to jest przestrzeganie logiki, którą wykorzystaliśmy na początku tego rozdziału i dodanie nowych funkcji do naszego zestawu danych. Tym razem dodamy zarówno drugą potęgę x, jak i trzecią potęgę x, aby dać sobie więcej możliwości poruszania się. Jak widać tutaj, ta zmiana znacznie poprawia naszą moc predykcyjną:
df <- transform(df, X2 = X ^ 2)
df <- transform(df, X3 = X ^ 3)
summary(lm(Y ~ X + X2 + X3, data = df))
#Call:
#lm(formula = Y ~ X + X2 + X3, data = df)
#
#Residuals:
# Min 1Q Median 3Q Max
#-0.32331 -0.08538 0.00652 0.08320 0.20239
#
#Coefficients:
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) -0.16341 0.04425 -3.693 0.000367 ***
#X 11.67844 0.38513 30.323 < 2e-16 ***
#X2 -33.94179 0.89748 -37.819 < 2e-16 ***
#X3 22.59349 0.58979 38.308 < 2e-16 ***
#—
#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
#Residual standard error: 0.1153 on 97 degrees of freedom
#Multiple R-squared: 0.9745, Adjusted R-squared: 0.9737
#F-statistic: 1235 on 3 and 97 DF, p-value: < 2.2e-16
Dodając jeszcze dwa dane wejściowe, przeszliśmy z R2 60% do R2 97%. To ogromny wzrost. Zasadniczo nie ma powodu, dla którego nie możemy przestrzegać tej logiki tak długo, jak chcemy, i dodawać kolejne moce X do naszego zestawu danych. Ale gdy dodamy więcej mocy, w końcu zaczniemy mieć więcej danych wejściowych niż punktów danych. Jest to zwykle niepokojące, ponieważ oznacza, że możemy w zasadzie idealnie dopasować nasze dane. Ale wcześniej pojawi się bardziej subtelny problem z tą strategią: nowe kolumny, które dodajemy do naszych danych, są tak podobne pod względem wartości do oryginalnych kolumn, że po prostu przestaną działać. W wynikach podsumowania pokazanych poniżej zobaczysz, że problem został rozwiązany jako „osobliwość”.
df <- transform(df, X4 = X ^ 4)
df <- transform(df, X5 = X ^ 5)
df <- transform(df, X6 = X ^ 6)
df <- transform(df, X7 = X ^ 7)
df <- transform(df, X8 = X ^ 8)
df <- transform(df, X9 = X ^ 9)
df <- transform(df, X10 = X ^ 10)
df <- transform(df, X11 = X ^ 11)
df <- transform(df, X12 = X ^ 12)
df <- transform(df, X13 = X ^ 13)
df <- transform(df, X14 = X ^ 14)
df <- transform(df, X15 = X ^ 15)
summary(lm(Y ~ X + X2 + X3 + X4 + X5 + X6 + X7 + X8 + X9 + X10 + X11 + X12 + X13 +
X14, data = df))
#Call:
#lm(formula = Y ~ X + X2 + X3 + X4 + X5 + X6 + X7 + X8 + X9 +
# X10 + X11 + X12 + X13 + X14, data = df)
#
#Residuals:
# Min 1Q Median 3Q Max
#-0.242662 -0.038179 0.002771 0.052484 0.210917
#
#Coefficients: (1 not defined because of singularities)
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) -6.909e-02 8.413e-02 -0.821 0.414
#X 1.494e+01 1.056e+01 1.415 0.161
#X2 -2.609e+02 4.275e+02 -0.610 0.543
#X3 3.764e+03 7.863e+03 0.479 0.633
#X4 -3.203e+04 8.020e+04 -0.399 0.691
#X5 1.717e+05 5.050e+05 0.340 0.735
#X6 -6.225e+05 2.089e+06 -0.298 0.766
#X7 1.587e+06 5.881e+06 0.270 0.788
#X8 -2.889e+06 1.146e+07 -0.252 0.801
#X9 3.752e+06 1.544e+07 0.243 0.809
#X10 -3.398e+06 1.414e+07 -0.240 0.811
#X11 2.039e+06 8.384e+06 0.243 0.808
#X12 -7.276e+05 2.906e+06 -0.250 0.803
#X13 1.166e+05 4.467e+05 0.261 0.795
#X14 NA NA NA NA
#
#Residual standard error: 0.09079 on 87 degrees of freedom
#Multiple R-squared: 0.9858, Adjusted R-squared: 0.9837
#F-statistic: 465.2 on 13 and 87 DF, p-value: < 2.2e-16
Problem polega na tym, że nowe kolumny, które dodajemy z coraz większymi potęgami X, są tak skorelowane ze starymi kolumnami, że algorytm regresji liniowej rozpada się i nie może znaleźć współczynników dla wszystkich kolumn osobno. Na szczęście istnieje rozwiązanie tego problemu, które można znaleźć w literaturze matematycznej: zamiast naiwnie dodawać proste potęgi x, dodajemy bardziej skomplikowane warianty x, które działają jak kolejne potęgi x, ale nie są ze sobą skorelowane tak jak x i x ^ 2. Te warianty na potęgach x są nazywane wielomianami ortogonalnymi, 1 i można je łatwo wygenerować za pomocą funkcji poly w R. Zamiast bezpośredniego dodawania 14 potęg x do ramki danych, wystarczy wpisać poly (X, stopień = 14) przekształcić x w coś podobnego do X + X ^ 2 + X ^ 3 + … + X ^ 14, ale z ortogonalnymi kolumnami, które nie wygenerują osobliwości podczas uruchamiania lm. Aby upewnić się, że poly czarna skrzynka działa poprawnie, możesz uruchomić lm z wyjściem z poly i przekonać się, że w rzeczywistości da ci właściwe współczynniki dla wszystkich 14 potęg X:
summary(lm(Y ~ poly(X, degree = 14), data = df))
#Call:
#lm(formula = Y ~ poly(X, degree = 14), data = df)
#
#Residuals:
# Min 1Q Median 3Q Max
#-0.232557 -0.042933 0.002159 0.051021 0.209959
#
#Coefficients:
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 0.010167 0.009038 1.125 0.2638
#poly(X, degree = 14)1 -5.455362 0.090827 -60.063 < 2e-16 ***
#poly(X, degree = 14)2 -0.039389 0.090827 -0.434 0.6656
#poly(X, degree = 14)3 4.418054 0.090827 48.642 < 2e-16 ***
#poly(X, degree = 14)4 -0.047966 0.090827 -0.528 0.5988
#poly(X, degree = 14)5 -0.706451 0.090827 -7.778 1.48e-11 ***
#poly(X, degree = 14)6 -0.204221 0.090827 -2.248 0.0271 *
#poly(X, degree = 14)7 -0.051341 0.090827 -0.565 0.5734
#poly(X, degree = 14)8 -0.031001 0.090827 -0.341 0.7337
#poly(X, degree = 14)9 0.077232 0.090827 0.850 0.3975
#poly(X, degree = 14)10 0.048088 0.090827 0.529 0.5979
#poly(X, degree = 14)11 0.129990 0.090827 1.431 0.1560
#poly(X, degree = 14)12 0.024726 0.090827 0.272 0.7861
#poly(X, degree = 14)13 0.023706 0.090827 0.261 0.7947
#poly(X, degree = 14)14 0.087906 0.090827 0.968 0.3358
#—
#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
#Residual standard error: 0.09083 on 86 degrees of freedom
#Multiple R-squared: 0.986, Adjusted R-squared: 0.9837
#F-statistic: 431.7 on 14 and 86 DF, p-value: < 2.2e-16
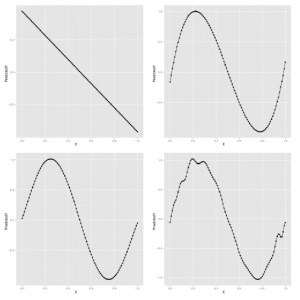
Ogólnie rzecz biorąc, poly daje dużą moc ekspresji. Matematycy wykazali, że regresja wielomianowa pozwoli ci uchwycić ogromną różnorodność skomplikowanych kształtów w twoich danych. Ale to niekoniecznie jest dobra rzecz. Jednym ze sposobów przekonania się, że dodatkowa moc zapewniana przez poli może być źródłem problemów, jest przyjrzenie się kształtowi modeli generowanych przez poli w miarę zwiększania parametru stopnia. W poniższym przykładzie generujemy modele przy użyciu poli ze stopniami 1, 3, 5 i 25. Wyniki pokazano w panelach tu
poly.fit <- lm(Y ~ poly(X, degree = 1), data = df)
df <- transform(df, PredictedY = predict(poly.fit))
ggplot(df, aes(x = X, y = PredictedY)) +
geom_point() +
geom_line()
poly.fit <- lm(Y ~ poly(X, degree = 3), data = df)
df <- transform(df, PredictedY = predict(poly.fit))
ggplot(df, aes(x = X, y = PredictedY)) +
geom_point() +
geom_line()
poly.fit <- lm(Y ~ poly(X, degree = 5), data = df)
df <- transform(df, PredictedY = predict(poly.fit))
ggplot(df, aes(x = X, y = PredictedY)) +
geom_point() +
geom_line()
poly.fit <- lm(Y ~ poly(X, degree = 25), data = df)
df <- transform(df, PredictedY = predict(poly.fit))
ggplot(df, aes(x = X, y = PredictedY)) +
geom_point() +
geom_line()
Możemy kontynuować ten proces w nieskończoność, ale patrząc na przewidywane wartości dla naszego modelu wyraźnie widać, że ostatecznie dopasowany kształt nie przypomina już fali, ale zaczyna być zniekształcany przez załamania i skoki. Problem polega na tym, że używamy modelu, który jest potężniejszy niż dane są w stanie obsłużyć. Rzeczy działają dobrze dla mniejszych stopni, takich jak 1, 3 lub 5, ale zaczynają się łamać wokół stopnia 25. Problem, który widzimy, to istota nadmiernego dopasowania. W miarę wzrostu liczby naszych obserwacji możemy pozwolić sobie na zastosowanie mocniejszych modeli. Ale dla każdego określonego zestawu danych zawsze istnieją modele, które są zbyt potężne. Jak możemy zrobić coś, aby to zatrzymać? I w jaki sposób możemy lepiej zrozumieć, co pójdzie nie tak, jeśli damy sobie wystarczająco dużo liny, aby się powiesić? Zaproponujemy odpowiedź na połączenie walidacji krzyżowej i legalizacji, dwóch najważniejszych narzędzi w całym zestawie narzędzi do uczenia maszynowego.