Relacje nieliniowe między kolumnami: poza liniami prostymi
Chociaż powiedzieliśmy ci prawdę , kiedy powiedzieliśmy, że regresja liniowa zakłada, że związek między dwiema zmiennymi jest linią prostą, okazuje się, że możesz również zobaczyć regresję liniową, aby uchwycić relacje, które nie są dobrze opisane linią prostą . Aby pokazać, co mamy na myśli, wyobraź sobie, że masz dane pokazane w panelu A na rysunku poniżej
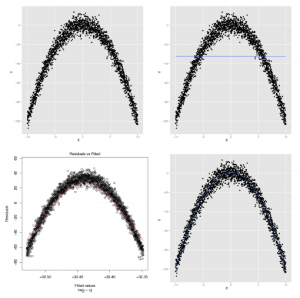
Patrząc na ten wykres rozrzutu jest oczywiste, że związek między X i Y nie jest dobrze opisany linią prostą. Rzeczywiście, wykreślenie linii regresji pokazuje nam dokładnie, co pójdzie źle, jeśli spróbujemy użyć linii do przechwycenia wzorca w tych danych; panel B na powyższym rysunku pokazuje wynik. Widzimy, że popełniamy błędy systematyczne w naszych prognozach, jeśli zastosujemy linię prostą: przy małych i dużych wartościach x przekraczamy y, a niedoceniamy średnich wartości x. Najłatwiej to zobaczyć na wykresie resztek, jak pokazano w panelu C na powyższym rysunku.
Na tym wykresie można zobaczyć całą strukturę oryginalnego zestawu danych, ponieważ żadna ze struktur nie jest przechwytywana przez domyślny model regresji liniowej. Korzystając z funkcji geom_smooth ggplot2 bez argumentu metody, możemy dopasować bardziej złożony model statystyczny zwany Uogólnionym modelem addytywnym (w skrócie GAM), który zapewnia płynną, nieliniową reprezentację struktury w naszych danych:
set.seed (1)
x <- seq (-10, 10, przez = 0,01)
y <- 1 – x ⋀ 2 + rnorm (długość (x), 0, 5)
ggplot (data.frame (X = x, Y = y), aes (x = X, y = Y)) +
geom_point () +
geom_smooth (se = FALSE)
Wynik pokazany w panelu D na powyższym rysunku pozwala nam od razu zobaczyć, że chcemy dopasować linię krzywą zamiast linii prostej do tego zestawu danych. Jak więc dopasować jakąś krzywą linię do naszych danych? Tutaj pojawiają się subtelności regresji liniowej: regresja liniowa może pasować tylko do linii na wejściu, ale można tworzyć nowe dane wejściowe, które są nieliniowymi funkcjami oryginalnych danych wejściowych. Na przykład możesz użyć następującego kodu w R, aby utworzyć nowe dane wejściowe na podstawie surowego wejścia x, który jest kwadratem surowego wejścia:
x.squared <- x ^ 2
Następnie możesz narysować y względem nowego wejścia x.squared, aby zobaczyć, jak z twoich danych wyłania się zupełnie inny kształt:
ggplot (data.frame (XSquared = x.squared, Y = y), aes (x = XSquared, y = Y)) + geom_point () + geom_smooth (method = ‘lm’, se = FALSE)
Jak pokazano na rysunku
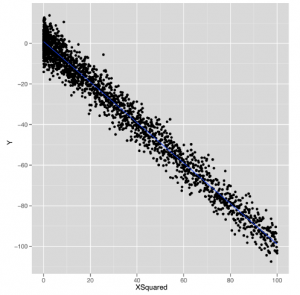
wykreślenie y względem tego nowego wejścia x.squared daje nam dopasowanie, które wygląda dokładnie jak linia prosta. Zasadniczo przekształciliśmy nasz pierwotny problem nieliniowy w nowy problem, w którym związek między dwoma wejściami naprawdę spełnia założenie liniowości regresji liniowej. Pomysł zastąpienia skomplikowanego problemu nieliniowego prostszym problemem liniowym z wykorzystaniem transformacji danych wejściowych pojawia się wielokrotnie w uczeniu maszynowym. Rzeczywiście, ta intuicja jest istotą sztuczki jądra, którą omówimy później. Aby zobaczyć, jak bardzo ta prosta transformacja do kwadratu poprawia naszą jakość przewidywania, możemy porównać wartości R2 dla regresji liniowych za pomocą xi x.squared:
podsumowanie (lm (y ~ x)) $ r.squared
# [1] 2.973e-06
podsumowanie (lm (y ~ x.squared)) $ r.squared
# [1] 0,9707
Przeszliśmy od rozliczania 0% wariancji do rozliczania 97%. To całkiem spory skok dla tak prostej zmiany w naszym modelu. Ogólnie rzecz biorąc, możemy się zastanawiać, o ile więcej mocy predykcyjnej możemy uzyskać, stosując bardziej ekspresyjne modele o bardziej skomplikowanych kształtach niż linie. Z powodów matematycznych, które wykraczają poza nasz zakres, okazuje się, że można uchwycić zasadniczo każdy rodzaj relacji, która mogłaby istnieć między dwiema zmiennymi przy użyciu bardziej złożonych zakrzywionych kształtów. Jedno podejście do budowania bardziej skomplikowanych kształtów nosi nazwę regresji wielomianowej, którą opiszemy w następnej części. Ale elastyczność zapewniana przez regresję wielomianową nie jest czysto dobrą rzeczą, ponieważ zachęca nas do naśladowania szumu w naszych danych dzięki naszemu dopasowanemu modelowi, a nie tylko prawdziwemu wzorcowi, który chcemy odkryć. Pozostała część skupi się na dodatkowych formach dyscypliny, które musimy ćwiczyć, jeśli będziemy używać bardziej złożonych narzędzi, takich jak regresja wielomianowa zamiast prostego narzędzia, takiego jak regresja liniowaa