Teraz, gdy wprowadziliśmy regresję liniową, zróbmy szybką dygresję, aby bardziej szczegółowo omówić słowo „korelacja”. W najściślejszym sensie dwie zmienne są skorelowane, jeśli związek między nimi można opisać za pomocą linii prostej. Innymi słowy, korelacja jest tylko miarą tego, jak dobrze można zastosować regresję liniową do modelowania zależności między dwiema zmiennymi. Korelacja 0 wskazuje, że nie ma interesującej linii, która łączy dwie zmienne. Korelacja 1 wskazuje, że istnieje idealnie dodatnia linia prosta (w górę), która wiąże dwie zmienne. A korelacja –1 wskazuje, że istnieje idealnie ujemna linia prosta (zejście w dół), która wiąże te dwie zmienne. Aby wszystko było precyzyjne, przejrzyjmy krótki przykład. Najpierw wygenerujemy dane, które nie są ściśle liniowe, a następnie wykreślimy je:
x <- 1:10
y <- x ^ 2
ggplot (data.frame (X = x, Y = y), aes (x = X, y = Y)) +
geom_point () +
geom_smooth (method = ‘lm’, se = FALSE)
Te przykładowe dane pokazano na rysunku
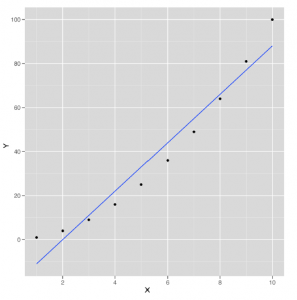
Jak widać, linia narysowana za pomocą geom_smooth nie przechodzi przez wszystkie punkty, więc relacja między x i y nie może być idealnie liniowa. Ale jak blisko jest? Aby odpowiedzieć na to pytanie, obliczamy korelację w R za pomocą funkcji cor:
cor (x, y)
# [1] 0,9745586
Tutaj widzimy, że x i y można całkiem dobrze powiązać za pomocą linii prostej. Funkcja cor pozwala oszacować, jak silny jest ten związek. W tym przypadku jest to 0,97, czyli prawie 1. Jak moglibyśmy obliczyć korelację dla siebie, zamiast używać kor? Możemy to zrobić za pomocą lm, ale najpierw musimy przeskalować zarówno x, jak i y. Skalowanie polega na odjęciu średniej obu zmiennych, a następnie podzieleniu przez odchylenie standardowe. Możesz wykonać
skalowanie w R za pomocą funkcji skalowania:
coef (lm (skala (y) ~ skala (x)))
Skala # (przechwytująca) (x)
# -1.386469e-16 9.745586e-01
Jak widać, w tym przypadku korelacja między x i y jest dokładnie równa współczynnikowi odnoszącemu się do nich w regresji liniowej po skalowaniu obu z nich. Jest to ogólny fakt na temat działania korelacji, dlatego zawsze możesz użyć regresji liniowej, aby pomóc ci dokładnie wyobrazić sobie, co to znaczy, że dwie zmienne mają być skorelowane. Ponieważ korelacja jest tylko miarą liniowości zależności między dwiema zmiennymi, nie mówi nam nic o przyczynowości. Prowadzi to do maksymy, że „korelacja nie jest przyczyną”. Niemniej jednak bardzo ważne jest, aby wiedzieć, czy dwie rzeczy są skorelowane, jeśli chcesz użyć jednej z nich do przewidywania drugiej. To kończy nasze wprowadzenie do regresji liniowej i pojęcia korelacji. Później pokażemy, jak uruchomić znacznie bardziej wyrafinowane modele regresji, które mogą obsługiwać wzorce nieliniowe w danych i jednocześnie zapobiegać nadmiernemu dopasowaniu.