Dwa największe założenia, które przyjmujemy przy użyciu regresji liniowej do przewidywania wyników, są następujące:
Rozdzielność / addytywność
Jeśli istnieje wiele informacji, które mogłyby wpłynąć na nasze domysły, zgadujemy, sumując efekty każdej informacji, tak jakby każda informacja była używana osobno. Na przykład, jeśli alkoholicy żyją o rok mniej niż osoby niebędące alkoholikami, a palacze żyją pięć lat mniej niż osoby niepalące, alkoholik, który jest także palaczem, powinien żyć 1 + 5 = 6 lat mniej niż niepalący. Założenie, że skutki rzeczy w izolacji sumują się, gdy zdarzają się razem, jest bardzo dużym założeniem, ale jest dobrym miejscem do rozpoczęcia wielu zastosowań regresji. Później porozmawiamy o idei interakcji, która jest techniką obejścia założenia separowalności w regresji liniowej, gdy na przykład wiesz, że efekt nadmiernego picia jest znacznie gorszy, jeśli również palisz.
Monotoniczność / liniowość
Model jest monotoniczny, gdy zmiana jednego z wejść zawsze powoduje wzrost lub spadek przewidywanej mocy wyjściowej. Na przykład, jeśli przewidujesz ciężary, używając wysokości jako danych wejściowych, a Twój model jest monotoniczny, to zakładasz, że za każdym razem, gdy wzrost kogoś wzrośnie, Twoja prognoza jego masy wzrośnie. Monotoniczność jest silnym założeniem, ponieważ można sobie wyobrazić wiele przykładów, w których moc wyjściowa rośnie nieco z wejściem, a następnie zaczyna spadać, ale założenie monotoniczności jest w rzeczywistości znacznie mniej silne niż pełne założenie algorytmu regresji liniowej, który nazywa się liniowością. Liniowość jest terminem technicznym o bardzo prostym znaczeniu: jeśli wykreślisz dane wejściowe i wyjściowe na wykresie rozrzutu, powinieneś zobaczyć linię, która wiąże dane wejściowe z danymi wyjściowymi, a nie coś o bardziej skomplikowanym kształcie, takim jak krzywa lub fala. Dla tych, którzy myślą mniej wizualnie, liniowość oznacza, że zmiana wejścia o jedną jednostkę zawsze dodaje N jednostek do wyjścia lub zawsze odejmuje N jednostek od wyjścia. Każdy model liniowy jest monotoniczny, ale krzywe mogą być monotoniczne bez liniowości. Z tego powodu liniowość jest bardziej restrykcyjna niż monotoniczność. Wyjaśnijmy dokładnie, co mamy na myśli, gdy mówimy linię, krzywą i falę, patrząc na przykłady wszystkich trzech na rysunku

Zarówno krzywe, jak i linie są monotoniczne, ale fale nie są monotoniczne, ponieważ czasami wznoszą się i opadają. Standardowa regresja liniowa będzie działać tylko wtedy, gdy dane będą wyglądać jak linia, gdy wydrukujesz dane wyjściowe względem każdego z danych wejściowych. W rzeczywistości można zastosować regresję liniową do dopasowania krzywych i fal, ale jest to bardziej zaawansowany temat, o którym będziemy mówić później.
Mając na uwadze założenia dotyczące addytywności i liniowości, zacznijmy od prostego przykładu regresji liniowej. Wróćmy do korzystania z naszych zestawów danych dotyczących wysokości i wag jeszcze raz, aby pokazać, jak regresja liniowa działa w tym kontekście. Na rycinie widzimy wykres rozrzutu, który narysowaliśmy wiele razy wcześniej.
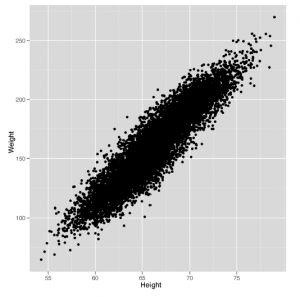
Niewielka zmiana naszego kodu kreślarskiego pokaże nam linię, którą wytworzy model regresji liniowej jako metodę przewidywania wag za pomocą wysokości, jak pokazano na rysunku
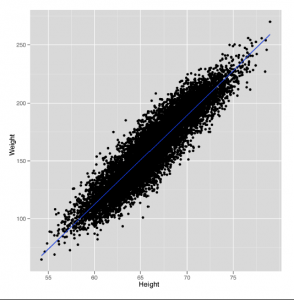
Po prostu musimy dodać wywołanie do funkcji geom_smooth, określając, że chcemy użyć metody lm, która implementuje „modele liniowe”.
library(‘ggplot2’)
heights.weights <- read.csv(‘data/01_heights_weights_genders.csv’,
header = TRUE,
sep = ‘,’)
ggplot(heights.weights, aes(x = Height, y = Weight)) +
geom_point() +
geom_smooth(method = ‘lm’)
Spojrzenie na ten wykres powinno Cię przekonać, że użycie linii do przewidzenia masy osoby, biorąc pod uwagę jej wzrost, może działać całkiem dobrze. Na przykład linia, którą widzimy, mówi, że powinniśmy przewidzieć wagę 105 funtów dla kogoś, kto ma 60 cali wzrostu, i powinniśmy przewidzieć wagę 225 funtów dla kogoś, kto ma 75 cali wzrostu. Rozsądne wydaje się zatem zaakceptowanie, że używanie linii do prognozowania jest mądrym posunięciem. W związku z tym pytanie, na które musimy odpowiedzieć, brzmi: „Jak znaleźć liczby określające linię, którą widzimy na tym wykresie?” W tym miejscu R naprawdę błyszczy jako język uczenia maszynowego: istnieje prosta funkcja o nazwie lm w R, która wykona za nas całą pracę. Aby użyć lm, musimy określić formułę regresji za pomocą operatora ~. W naszym przykładzie zamierzamy przewidzieć wagę na podstawie wzrostu, więc piszemy Waga ~ wzrost. Gdybyśmy mieli przewidywać w przeciwnym kierunku, zapisalibyśmy Wzrost ~ Waga. Jeśli chcesz wymawiać te formuły, osobiście lubimy mówić, że Wzrost ~ Waga oznacza „wzrost jako funkcja wagi”. Oprócz specyfikacji regresji musimy powiedzieć R, gdzie jesteśmy danymi korzystanie jest przechowywane. Jeśli zmienne w regresji są zmiennymi globalnymi, możesz to pominąć, ale społeczność R. nie lubi tego typu zmiennych globalnych. Przechowywanie zmiennych globalnych w R jest uważane za złą praktykę, ponieważ łatwo jest zgubić to, co zostało załadowane do pamięci, a co nie. Może to powodować niezamierzone konsekwencje w kodowaniu, ponieważ łatwo jest stracić kontrolę nad tym, co znajduje się w pamięci i co z niej nie ma. Ponadto zmniejsza łatwość udostępniania kodu. Jeśli zmienne globalne nie są wyraźnie zdefiniowane w kodzie, ktoś, kto jest mniej zaznajomiony z procesem ładowania danych, może coś przeoczyć, w wyniku czego kod może nie działać, ponieważ brakuje jakiegoś zestawu danych lub zmiennej. Lepiej jest jawnie określić źródło danych za pomocą parametru danych. Zestawiając je razem, przeprowadzamy regresję liniową w R w następujący sposób:
fitted.regression <- lm(Weight ~ Height,
data = heights.weights)
Po uruchomieniu tego wywołania do lm możesz wyciągnąć punkt przecięcia linii regresji z wywołaniem funkcji coef, która zwraca współczynniki dla modelu liniowego, który odnosi dane wejściowe do wyników. Mówimy „model liniowy”, ponieważ regresja może działać w więcej niż dwóch wymiarach. W dwóch wymiarach dopasowujemy linie (stąd część „liniowa”), ale w trzech wymiarach dopasowujemy płaszczyzny, a w więcej niż trzech wymiarach dopasowujemy hiperpłaszczyzny.
Jeśli te terminy nic dla ciebie nie znaczą, intuicja jest prosta: płaska powierzchnia w dwóch wymiarach jest linią, podczas gdy w trzech wymiarach jest to płaszczyzna, aw więcej niż trzech wymiarach, płaska powierzchnia jest nazywana hiperpłaszczyzną. Jeśli nie jest to wystarczająco jasne, zalecamy przeczytanie Flatland.
coef(fitted.regression)
#(Intercept) Height
#-350.737192 7.717288
Zrozumienie tego wyniku jest w pewnym sensie rozumieniem regresji liniowej. Najprostszym sposobem na zrozumienie danych wyjściowych z cewki jest wyraźne zapisanie relacji, którą implikuje:
intercept <- coef(fitted.regression)[1]
slope <- coef(fitted.regression)[2]
# predicted.weight <- intercept + slope * observed.height
# predicted.weight == -350.737192 + 7.717288 * observed.height
Oznacza to, że każdy wzrost 1 cala wzrostu kogoś powoduje wzrost jego masy o 7,7 funta. To wydaje nam się dość rozsądne. W przeciwieństwie do tego, przechwytywanie jest nieco dziwniejsze, ponieważ mówi ci, ile waży osoba o wzroście 0 cali. Według R. ważyłaby –350 funtów. Jeśli chcesz zrobić algebrę, możesz wywnioskować, że dana osoba musi mieć 45 cali wysokości, aby nasz algorytm przewidywania powiedział, że waży 0 funtów. Krótko mówiąc, nasz model regresji nie jest tak świetny dla dzieci ani wyjątkowo niskich dorosłych. Jest to w rzeczywistości systematyczny problem regresji liniowej w ogólności: modele predykcyjne zwykle nie są zbyt dobre w przewidywaniu wyników dla danych wejściowych, które są bardzo dalekie od wszystkich danych wejściowych, które widziałeś w przeszłości. Często możesz popracować poprawić jakość zgadywania poza zakresem danych używanych do trenowania modelu, ale w tym przypadku prawdopodobnie nie ma takiej potrzeby, ponieważ zazwyczaj będziesz przewidywał tylko osoby, które mają ponad 4 ‘i poniżej 8’ wzrostu . Oprócz prowadzenia regresji i analizowania uzyskanych współczynników, w R można zrobić znacznie więcej, aby zrozumieć wyniki regresji liniowej. Przejrzenie wszystkich różnych wyników, które może wytworzyć R, zajęłoby całą książkę, więc skupimy się na kilku najważniejszych częściach po wyodrębnieniu współczynników. Gdy tworzysz prognozy w praktycznym kontekście, wszystkie współczynniki są wszystkim, co musisz wiedzieć. Po pierwsze, chcemy dowiedzieć się, gdzie nasz model jest zły. Robimy to, obliczając prognozy modelu i porównując je z danymi wejściowymi. Aby znaleźć przewidywania modelu, używamy funkcji przewidywania w R:
predict(fitted.regression)
Kiedy już mamy nasze przewidywania, możemy obliczyć różnicę między naszymi przewidywaniami a prawdą za pomocą prostego odejmowania:
true.values <- with(heights.weights,Weight)
errors <- true.values – predict(fitted.regression)
Błędy, które obliczamy w ten sposób, nazywane są resztkami, ponieważ stanowią one część naszych danych, które pozostały po uwzględnieniu części, którą wiersz może wyjaśnić. Możesz uzyskać te reszty bezpośrednio w R bez funkcji przewidywania, używając zamiast tego funkcji reszty:
residuals(fitted.regression)
Typowym sposobem diagnozowania oczywistych błędów, które popełniamy podczas regresji liniowej, jest wykreślanie resztek względem prawdy:
plot(fitted.regression, which = 1)
W tym miejscu poprosiliśmy R, aby wykreślił tylko pierwszy wykres diagnostyczny regresji, określając, który = 1. Istnieją inne wykresy, które można uzyskać, i zachęcamy do eksperymentowania, aby sprawdzić, czy któryś z pozostałych jest pomocny. W tym przykładzie możemy stwierdzić, że nasz model liniowy działa dobrze, ponieważ w resztach nie ma systematycznej struktury. Ale oto inny przykład, w którym linia jest nieodpowiednia:
x <- 1:10
y <- x ^ 2
fitted.regression <- lm(y ~ x)
plot(fitted.regression, which = 1)
Widzimy oczywistą strukturę w pozostałościach tego problemu. Zasadniczo jest to złe podczas modelowania danych: model powinien podzielić świat na sygnał (który daje ci dyktando) i hałas (który daje reszty). Jeśli gołym okiem widzisz sygnał w resztkach, oznacza to, że Twój model nie jest wystarczająco silny, aby wyodrębnić cały sygnał i pozostawić jedynie prawdziwy szum jako resztki. Aby rozwiązać ten problem, później omówimy mocniejsze modele regresji niż prosty model regresji liniowej, nad którym obecnie pracujemy. Ponieważ jednak wielka moc niesie ze sobą wielką odpowiedzialność, skupimy się na unikatowych problemach, które pojawiają się, gdy używamy modeli tak potężnych, że w rzeczywistości są zbyt potężne, aby można było z nich korzystać bez ostrożności. Na razie porozmawiajmy dokładniej o tym, jak dobrze sobie radzimy z regresją liniową. Posiadanie resztek jest świetne, ale jest ich tak wiele, że praca z nimi może być przytłaczająca. Chcielibyśmy, aby jedna liczba podsumowała jakość naszych wyników. Najprostszym pomiarem błędu jest (1) pobranie wszystkich reszt, (2) wyprostowanie ich w celu uzyskania kwadratowych błędów dla naszego modelu i (3) zsumowanie ich.
x <- 1:10
y <- x ^ 2
fitted.regression <- lm(y ~ x)
errors <- residuals(fitted.regression)
squared.errors <- errors ^ 2
sum(squared.errors)
#[1] 528
Ta prosta suma kwadratów błędów jest przydatna do porównywania różnych modeli, ale ma pewne dziwactwa, których większość ludzi nie lubi.
Po pierwsze, suma błędów kwadratu jest większa dla dużych zbiorów danych niż dla małych zbiorów danych. Aby się o tym przekonać, wyobraź sobie ustalony zestaw danych i sumę kwadratów błędów dla tego zestawu danych. Teraz dodaj jeszcze jeden punkt danych, który nie jest dokładnie przewidziany. Ten nowy punkt danych musi zwiększyć sumę błędów podniesionych do kwadratu, ponieważ dodanie liczby do poprzedniej sumy błędów kwadratu może tylko zwiększyć sumę. Istnieje jednak prosty sposób na rozwiązanie tego problemu: raczej wykorzystaj średnią z kwadratów błędów niż sumę. To daje nam miarę MSE, której używaliśmy wcześniej w tym rozdziale. Chociaż MSE nie będzie rosło konsekwentnie, ponieważ otrzymamy więcej danych, niż w przypadku surowej sumy błędów kwadratu, MSE nadal ma problem: jeśli średnia prognoza jest wyłączona tylko o 5, wtedy średni błąd kwadratu wyniesie 25. To dlatego, że wyrównujemy błędy, zanim wykorzystamy ich średnią.
x <- 1:10
y <- x ^ 2
dopasowanie. regresja <- lm (y ~ x)
błędy <- resztki (dopasowanie. regresja)
squared.errors <- błędy ^ 2
mse <- mean (squared.errors)
mse
# [1] 52,8
Rozwiązanie tego problemu skali jest trywialne: bierzemy pierwiastek kwadratowy średniego błędu kwadratu, aby uzyskać pierwiastek średni błąd kwadratu, czyli pomiar RMSE, który również wypróbowaliśmy wcześniej w tym rozdziale. RMSE jest bardzo popularną miarą wydajności do oceny algorytmów uczenia maszynowego, w tym algorytmów o wiele bardziej wyrafinowanych niż regresja liniowa. Tylko w jednym przykładzie nagrodę Netflix przyznano za pomocą RMSE jako ostatecznej miary skuteczności algorytmów uczestników.
x <- 1:10
y <- x ^ 2
dopasowanie. regresja <- lm (y ~ x)
błędy <- resztki (dopasowanie. regresja)
squared.errors <- błędy ^ 2
mse <- mean (squared.errors)
rmse <- sqrt (mse)
rmse
# [1] 7.266361
Jeden problem, którą ludzie mają z RMSE, polega na tym, że nie jest od razu jasne, co to jest mierna wydajność. Doskonała wydajność wyraźnie daje RMSE równą 0, ale dążenie do perfekcji nie jest realistycznym celem w tych zadaniach. Podobnie nie jest łatwo rozpoznać, kiedy model działa bardzo słabo. Na przykład, jeśli wszyscy mają wysokość 5, a przewidujesz 5000, otrzymasz ogromną wartość dla RMSE. Możesz zrobić coś gorszego, przewidując 50 000 „, a jeszcze gorzej, przewidując 5 000 000”. Nieograniczone wartości, które może przyjąć RMSE, utrudniają ustalenie, czy wydajność twojego modelu jest rozsądna.
Podczas regresji liniowych rozwiązaniem tego problemu jest użycie R2 (wymawiane „R do kwadratu”). Ideą R2 jest sprawdzenie, o ile lepszy jest Twój model, niż gdybyśmy tylko użyli tego środka. Aby ułatwić interpretację, R2 zawsze będzie zawierać się w przedziale od 0 do 1. Jeśli nie masz nic lepszego niż średnia, będzie wynosić 0. każdy punkt danych idealnie, R2 będzie wynosić 1. Ponieważ R2 ma zawsze wartość od 0 do 1, ludzie mają tendencję do mnożenia go przez 100 i mówią, że jest to procent wariancji w danych, które wyjaśniłeś swoim modelem. To jest wygodny sposób budowania intuicji na temat dokładności modelu, nawet w nowej domenie, w której nie masz doświadczenia w zakresie standardowych wartości RMSE. Aby obliczyć R2, musisz obliczyć RMSE dla modelu, który wykorzystuje tylko średnią wydajność do prognozowania dla wszystkich przykładowych danych. Następnie musisz obliczyć RMSE dla swojego modelu. Następnie jest to prosta operacja arytmetyczna na utworzenie R2, którą opisaliśmy w kodzie tutaj:
mean.rmse <- 1.09209343
model.rmse <- 0,954544
r2 <- 1 – (model.rmse / mean.rmse)
r2
# [1] 0,12559502