To może wydawać się głupie, ale najprostszym możliwym sposobem wykorzystania informacji, które mamy jako dane wejściowe, jest całkowite zignorowanie danych wejściowych i przewidywanie przyszłych wyników na podstawie jedynie średniej wartości wyników, które widzieliśmy w przeszłości. W przykładzie aktuariusza możemy całkowicie zignorować dokumentację medyczną osoby i po prostu zgadnąć, że będzie ona żyła tak długo, jak żyje przeciętna osoba. Zgadywanie średniego wyniku dla każdego przypadku nie jest tak naiwne, jak mogłoby się wydawać: jeśli jesteśmy zainteresowani prognozami, które są jak najbliższe prawdy, jak to możliwe, bez korzystania z innych informacji, zgadywanie średniego wyniku okazuje się najlepsze Chyba możemy to zrobić. Trochę pracy wymaga zdefiniowania „najlepszego”, aby nadać temu twierdzeniu określone znaczenie. Jeśli czujesz się niekomfortowo, gdy rzucamy słowo „najlepszy”, nie mówiąc o tym, co mamy na myśli, obiecujemy, że wkrótce podamy formalną definicję. Zanim omówimy, jak najlepiej zgadywać, załóżmy, że mamy dane z wyimaginowanej bazy danych aktuarialnych, której część pokazano w tabelce:
Palił : Wiek w chwili śmierci
1 : 75
1 : 72
1 : 66
1 : 74
1 : 69
… : …
0 : 66
0 : 80
0 : 84
0 : 63
0 : 79
… : …
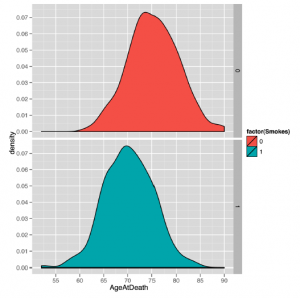
Ponieważ jest to zupełnie nowy zestaw danych, dobrze jest postępować zgodnie z naszymi sugestiami w bardziej szczegółowej części i eksplorować dane przed przeprowadzeniem jakiejkolwiek formalnej analizy. Mamy jedną kolumnę numeryczną i drugą kolumnę, która jest kodem obojętnym, więc naturalne jest tworzenie wykresów gęstości w celu porównania palaczy z osobami niepalącymi
ages <- read.csv (‘data / longevity.csv’)
ggplot (ages, aes (x = AgeAtDeath, fill = współczynnik (Smokes))) +
geom_density() +
facet_grid(Smokes ~ .)
Powstały w ten sposób wykres wydaje się uzasadniony, aby sądzić, że palenie ma znaczenie dla długowieczności, ponieważ środek rozkładu długości życia palaczy jest przesunięty w prawo od środka długości życia palaczy. Innymi słowy, średnia długość życia osoby niepalącej jest dłuższa niż średnia długość życia osoby palącej. Ale zanim opiszemy, w jaki sposób możesz wykorzystać posiadane przez nas informacje o nawykach palenia danej osoby, aby przewidzieć jej długość życia, udawajmy przez chwilę, że nie posiadałeś żadnej z tych informacji. W takim przypadku musisz wybrać jeden numer jako prognozę dla każdej nowej osoby, niezależnie od jej nawyków związanych z paleniem. Jaki numer wybrać? To pytanie nie jest trywialne, ponieważ liczba, którą powinieneś wybrać, zależy od tego, co Twoim zdaniem oznacza dobre przewidywanie. Istnieje wiele rozsądnych sposobów na określenie dokładności prognoz, ale istnieje jedna miara jakości, która dominowała praktycznie w całej historii statystyki. Miara ta nazywana jest błędem do kwadratu. Jeśli próbujesz przewidzieć wartość y (prawdziwy wynik) i zgadniesz h (twoja hipoteza na temat y), wtedy kwadratowy błąd zgadnięcia jest po prostu (y – h) ^ 2. Powyżej wartości nieodłącznie wynikającej z następujących konwencji zrozumiałe dla innych, istnieje wiele dobrych powodów, dla których warto zastosować kwadratowy błąd do pomiaru jakości domysłów. Nie zajmiemy się nimi teraz, ale porozmawiamy trochę więcej o sposobach pomiaru błędu, gdy mówimy o algorytmach optymalizacji w uczeniu maszynowym. Na razie postaramy się cię przekonać o czymś fundamentalnym: jeśli używamy błędu kwadratu do mierzenia jakości naszych prognoz, wtedy możemy zgadywać, jak długo możemy żyć na temat długości życia danej osoby – bez żadnych dodatkowych informacji o nawyki człowieka – to długość życia przeciętnego człowieka. Aby przekonać Cię o tym roszczeniu, zobaczmy, co się stanie, jeśli użyjemy innych domysłów zamiast średniej. Dzięki zestawowi danych dotyczących długowieczności średni AgeAtDeath wynosi 72,723, a na razie zaokrąglamy do 73. Możemy wtedy zapytać: „Jak źle przewidzielibyśmy wiek osób w naszym zbiorze danych, gdybyśmy zgadli, że wszyscy żyją w wieku 73 lat?” Aby odpowiedzieć na to pytanie w R, możemy użyć następującego kodu, który łączy wszystkie błędy kwadratowe dla każdej osoby w naszym zbiorze danych, obliczając średnią błędu kwadratowego, który nazywamy średnim błędem kwadratowym (lub MSE dla krótki):
ages <- read.csv(‘data/longevity.csv’)
guess <- 73
with(ages, mean((AgeAtDeath – guess) ^ 2))
#[1] 32.991
Po uruchomieniu tego kodu okazuje się, że średni błąd kwadratowy, który popełniamy zgadując 73 dla każdej osoby w naszym zestawie danych, wynosi 32,991. Ale to samo w sobie nie powinno być wystarczające, aby przekonać cię, że zrobilibyśmy gorzej z przypuszczeniem, że nie jest to 73. Aby przekonać cię, że 73 jest najlepszym przypuszczeniem, musimy zastanowić się, jak byśmy się zachowali, gdybyśmy coś zrobili innych możliwych domysłów. Aby obliczyć te inne wartości w R, zapętlamy sekwencję możliwych domysłów od 63 do 83:
ages <- read.csv(‘data/longevity.csv’)
guess.accuracy <- data.frame()
for (guess in seq(63, 83, by = 1))
{
prediction.error <- with(ages,
mean((AgeAtDeath – guess) ^ 2))
guess.accuracy <- rbind(guess.accuracy,
data.frame(Guess = guess,
Error = prediction.error))
}
ggplot(guess.accuracy, aes(x = Guess, y = Error)) +
geom_point() +
geom_line()
Jak widać z rysunku 5-2,
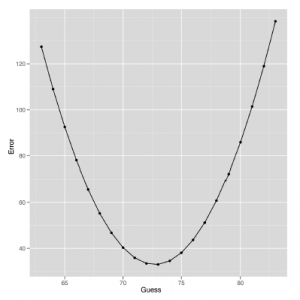
użycie jakichkolwiek domysłów innych niż 73 daje nam gorsze prognozy dla naszego zestawu danych. Jest to właściwie ogólny wynik teoretyczny, który można udowodnić matematycznie: aby zminimalizować błąd do kwadratu, chcesz przewidzieć średnią wartość w swoim zestawie danych. Jednym z ważnych implikacji tego jest to, że wartość predykcyjna posiadania informacji o paleniu powinna być mierzona w kategoriach stopnia poprawy, jaki uzyskujesz dzięki wykorzystaniu tych informacji w porównaniu z wykorzystaniem jedynie wartości średniej jako wartości domyślnej dla bardzo widocznej osoby.