Odpowiedź przychodzi w przekształcaniu skal. Musimy sprawić, by relacje liczbowe między jednostkami w naszym zestawie funkcji były mniej ekstremalne. Jeśli porównamy bezwzględne liczby częstotliwości, wiadomość e-mail od tim.one@comcast.ent będzie ważona jako 15 razy ważniejsza niż wiadomość e-mail od przeciętnego nadawcy. Jest to bardzo problematyczne, ponieważ będziemy chcieli ustalić próg bycia wiadomością priorytetową lub nie, w oparciu o zakres wartości masy wytworzonych przez naszego rankingowego na etapie uczenia się. Przy tak ekstremalnym skośności nasz próg będzie albo o wiele za niski, albo o wiele za wysoki, dlatego musimy przeskalować jednostki, aby uwzględnić charakter naszych danych. To prowadzi nas do logarytmów i transformacji logarytmów. Prawdopodobnie znasz logarytmy z matematyki elementarnej, ale jeśli nie, koncepcja jest dość prosta. Logarytm jest funkcją, która zwraca wartość wykładnika, która spełniałaby równanie, w którym liczba podstawowa podniesiona do tego wykładnika jest równa liczbie podanej funkcji logarytmicznej. Wartość podstawowa w transformacji logarytmów ma kluczowe znaczenie. Jako hakerzy znamy myślenie o rzeczy o podstawie dwa lub binarnej. Możemy bardzo łatwo skonstruować logarytmiczną transformację podstawy dwa. W takim przypadku rozwiązalibyśmy równanie wartości wykładniczej, gdzie wartość wejściowa jest równa dwóm podniesionym do tego wykładnika. Na przykład, jeśli przekształcimy 16 za pomocą logarytmu base-two, będzie to cztery, ponieważ dwa podniesione do czwartej potęgi wynoszą 16. Zasadniczo „odwracamy” wykładniczy, więc tego rodzaju transformacje działają najlepiej, gdy dane pasują do takich funkcja. Dwie najczęstsze transformacje logów to tak zwany log naturalny i transformacja log-base-10. W pierwszym przypadku podstawą jest specjalna wartość e, która jest stałą niewymierną (jak pi) równą około 2,718. Nazwa logarytm naturalny jest często oznaczana ln. Szybkości zmian tej stałej są bardzo często obserwowane w przyrodzie, a w rzeczywistości wyprowadzenie może być wykonane geometrycznie jako funkcja kątów wewnątrz koła. Prawdopodobnie bardzo dobrze znasz kształty i relacje zgodne z naturalnym dziennikiem, chociaż może nie pomyślałeś o nich w tych kategoriach. Rysunek ilustruje naturalną spiralę logarytmiczną, którą można zaobserwować w wielu naturalnie występujących zjawiskach. Niektóre przykłady obejmują wewnętrzną strukturę skorupy łodzika i spiralne wiatry huraganu (lub tornada).
Nawet rozproszenie cząstek międzygwiezdnych w naszej galaktyce następuje po naturalnej spirali logarytmicznej. Ponadto wiele otworów w ustawieniach profesjonalnych kamer różni się w zależności od logarytmów naturalnych. Biorąc pod uwagę intymny związek między tą wartością a wieloma naturalnie występującymi zjawiskami, jest to świetna funkcja do przeskalowywania danych społecznościowych – jako aktywności e-mail – która ma charakter wykładniczy. Alternatywnie, transformacja logarytmiczna podstawa-10, często oznaczana log10, zastępuje wartość e w naturalnej transformacji logarytmicznej 10. Biorąc pod uwagę, jak działa transformacja logarytmiczna, wiemy, że transformacja log-podstawa 10 zmniejszy duże wartości do znacznie mniejszych te niż naturalny dziennik. Na przykład transformacja logarytmu base-10 wynosząca 1000 wynosi 3, ponieważ 10 podniesiona do potęgi trzeciej to 1000, podczas gdy logarytm naturalny wynosi około 6,9. Dlatego sensowne jest użycie transformacji log-base-10, gdy nasze dane są skalowane według bardzo dużego wykładnik. Sposoby, w jakie obie te opcje przekształcą nasze dane dotyczące liczby wiadomości e-mail, pokazano na rysunku
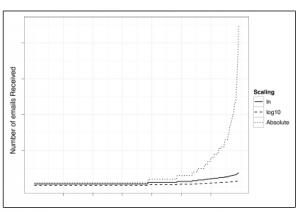
Na tym rysunku widzimy, że liczba wiadomości e-mail wysyłanych przez użytkowników w danych szkoleniowych jest dość gwałtowna. Przekształcając te wartości za pomocą logarytmu naturalnego i log-base-10, znacznie spłaszczamy tę linię. Jak wiemy, logarytm base-10 znacznie przekształca wartości, podczas gdy log naturalny wciąż zapewnia pewne zmiany, które pozwolą nam wyciągnąć znaczące wagi z tych danych treningowych. Z tego powodu użyjemy dziennika naturalnego, aby zdefiniować wagę naszej funkcji objętości e-maila.
Jak już to zrobiliśmy i jak szczegółowo wyjaśniliśmy wcześniej, zawsze dobrze jest eksplorować dane wizualnie podczas pracy przez jakikolwiek problem z uczeniem maszynowym. Chcemy wiedzieć, w jaki sposób wszystkie obserwacje w naszym zestawie funkcji odnoszą się do siebie w celu uzyskania najlepszych prognoz. Często najlepszym sposobem na to jest wizualizacja danych.
from.weight <- transform (from.weight, Weight = log (Freq + 1))
Na koniec przypomnij sobie z matematyki w szkole swoje zasady dotyczące wykładników. Wszystko podniesione do zera zawsze jest równe jeden. Jest to bardzo ważne, o czym należy pamiętać przy stosowaniu transformacji logarytmicznej w schemacie ważenia, ponieważ każda obserwacja równa jednej zostanie przekształcona na zero. Jest to problematyczne w schemacie ważenia, ponieważ pomnożenie innych wag przez zero spowoduje wyzerowanie całej wartości. Aby tego uniknąć, zawsze dodajemy jedną do wszystkich obserwacji przed pobraniem logów.
W R jest funkcja o nazwie log1p, która oblicza log (1 + p), ale dla celów uczenia się i wyrażania się, dodamy to „ręcznie”.
Biorąc pod uwagę przeskalowanie, nie wpływa to na nasze wyniki i utrzymuje wszystkie wagi powyżej zera. W tym przypadku używamy domyślnej wartości podstawowej dla funkcji dziennika, która jest dziennikiem naturalnym.
Dla naszych celów nigdy nie będziemy mieć obserwacji w naszym zestawie funkcji, która jest równa zero, ponieważ liczymy rzeczy. Jeśli nie ma żadnych obserwacji, to po prostu nie wprowadza naszych danych treningowych. W niektórych przypadkach nie będzie to jednak prawdą i możesz mieć zerowe obserwacje w swoich danych. Dziennik zerowy jest niezdefiniowany, a jeśli spróbujesz go obliczyć w R, zwróci specjalną wartość -Inf. Często występujące w danych -Inf powodują, że wszystko się wysadza.