Do tej pory omawialiśmy jedynie strategie przemyślanego przemyślenia poszczególnych kolumn w zbiorze danych. Jest to z pewnością warte zrobienia: często po prostu znajomość kształtu w danych mówi wiele o twoich danych. Obserwacja rozkładu normalnego mówi nam, że możesz używać wartości średniej i mediany zamiennie, a także oznacza, że możesz ufać, że przez większość czasu nie zobaczysz danych o więcej niż trzy standardowe odchylenia od średniej. To wiele do nauczenia się z jednej wizualizacji. Ale cały materiał, który właśnie sprawdziliśmy, jest tym, czego można się spodziewać w tradycyjnej klasie statystyki; nie ma wrażenia aplikacji do uczenia maszynowego, które prawdopodobnie swędzisz, aby zacząć się angażować. Aby przeprowadzić prawdziwe uczenie maszynowe, musimy znaleźć relacje między wieloma kolumnami w naszych danych i wykorzystać te relacje do zrozumienia naszych danych i przewidzenia przyszłości. Niektóre przykłady, które omówimy w trakcie tej książki, obejmują następujące problemy z prognozowaniem:
- Przewidywanie czyjejś wagi na podstawie jej wzrostu
- Przewidywanie, czy wiadomość e-mail jest spamem, czy nie używa jej tekstu
- Przewidywanie, czy użytkownik będzie chciał kupić produkt, którego nigdy wcześniej mu nie proponowałeś
Jak wspomnieliśmy wcześniej, tego rodzaju problemy dzielą się na dwa typy: problemy z regresją, w których należy przewidzieć pewną liczbę, na przykład wagę, biorąc pod uwagę wiele innych liczb, takich jak wzrost; oraz problemy z klasyfikacją, w których należy przypisać etykietę, taką jak spam, podając kilka liczb, na przykład liczbę słów dla spamerskich słów, takich jak „viagra” i „cialis”. Przedstawiamy narzędzia, których możemy użyć do regresji i klasyfikacji, zajmą większość reszty tej książki, ale istnieją dwa motywujące typy wizualizacji danych, które chcielibyśmy, abyś nosił je w głowie, gdy idziemy do przodu. Pierwszym z nich jest stereotypowy obraz regresji. Na obrazie regresji tworzymy wykres rozrzutu naszych danych i widzimy, że istnieje ukryty kształt, który łączy dwie kolumny w zbiorze danych. Wracając do naszych ulubionych danych o wysokościach i wagach, zróbmy wykres rozrzutu wag względem wysokości.
Jeśli ich nie znasz, powinieneś wiedzieć, że wykres rozproszenia to dwuwymiarowy obraz, w którym jeden wymiar odpowiada zmiennej X, a drugi zmiennej Y. Aby tworzyć nasze wykresy rozrzutu, będziemy nadal używać ggplot.
ggplot (heights.weights, aes (x = Height, y = Weight)) + geom_point ()
Wykres rozrzutu generowany przez ggplot pokazano tu
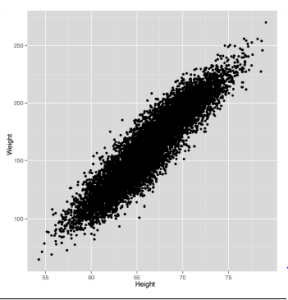
Patrząc na ten obraz, wydaje się całkiem jasne, że istnieje wzorzec odnoszący się do wysokości i ciężarów: ludzie wyżsi również ważą więcej. Jest to intuicyjnie oczywiste, ale opisanie ogólnych strategii znajdowania tego rodzaju wzorców zajmie resztę tego tekstu.
Aby dokładniej zbadać wzór, możemy użyć narzędzia wygładzającego
ggplot2, aby uzyskać wizualne przedstawienie wzorca liniowego, który widzimy:
ggplot (heights.weights, aes (x = Height, y = Weight)) + geom_point () + geom_smooth ()
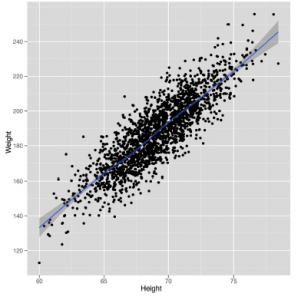
Nowy wykres rozproszenia z nałożonym gładkim wzorem pokazano tu
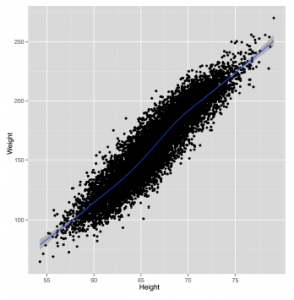
geom_smooth wygeneruje prognozy dotyczące masy ludzi na podstawie ich wysokości jako danych wejściowych. W tym przypadku prognozy są po prostu linią pokazaną na niebiesko. Wokół linii znajduje się zacieniony region, który opisuje inne prawdopodobne prognozy, które można by zrobić dla czyjejś wagi na podstawie danych, które widziałeś. W miarę zdobywania kolejnych danych domysły stają się dokładniejsze, a zacieniony region kurczy się. Ponieważ wykorzystaliśmy już wszystkie dane, najlepszym sposobem, aby zobaczyć ten efekt, jest pójście w przeciwnym kierunku: usuń część naszych danych i zobacz, jak wzór staje się coraz słabszy. Wyniki pokazano poniżej
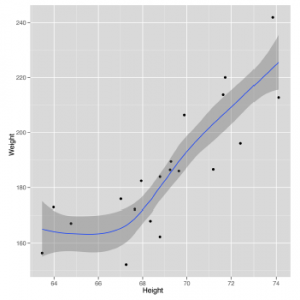
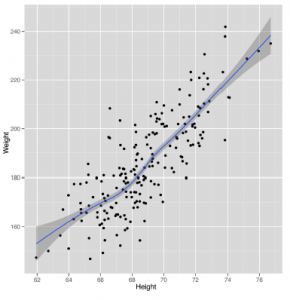
ggplot(heights.weights[1:20,], aes(x = Height, y = Weight)) + geom_point() +
geom_smooth()
ggplot(heights.weights[1:200,], aes(x = Height, y = Weight)) + geom_point() +
geom_smooth()
ggplot(heights.weights[1:2000,], aes(x = Height, y = Weight)) + geom_point() +
geom_smooth()
Przypomnij sobie, że przewidywanie wartości w jednej kolumnie przy użyciu innej kolumny nazywa się regresją, gdy wartości, które próbujesz przewidzieć, to liczby. Natomiast gdy próbujesz przewidzieć etykiety, nazywamy tę klasyfikację. Do klasyfikacji rysunek jest obrazem, o którym należy pamiętać.
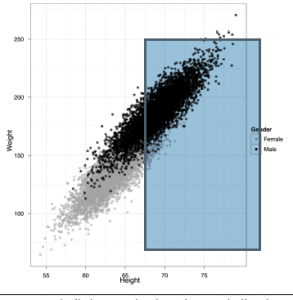
Na tym obrazie pokazaliśmy wysokości i wagi każdej osoby w naszym zbiorze danych, ale zwizualizowaliśmy również ich płeć jako kolor każdego punktu. To wyjaśnia, że w naszych danych widzimy dwie odrębne grupy osób. Aby wygenerować ten obraz w ggplot2, uruchamiamy następujący kod:
ggplot(heights.weights, aes(x = Height, y = Weight, color = Gender)) + geom_point()
Ten obraz jest standardowym obrazem klasyfikacyjnym. Na obrazie klasyfikacyjnym tworzymy wykres rozrzutu naszych danych, ale używamy trzeciej kolumny do pokolorowania punktów różnymi etykietami.
Do naszych danych dotyczących wzrostu i masy ciała dodaliśmy trzecią kolumnę, która przedstawia płeć każdej osoby w naszym zbiorze danych. Patrząc na to zdjęcie, prawdopodobnie wydaje się, że moglibyśmy odgadnąć płeć osoby, używając tylko jej wzrostu i wagi. Zgadywanie na temat zmiennych kategorialnych, takich jak płeć na podstawie innych danych, jest dokładnie tym, co powinna zrobić klasyfikacja, a opiszemy dla niej algorytmy bardziej szczegółowo w następnej części. Na razie pokażemy na rysunku 2-31, jak wyglądałyby wyniki po uruchomieniu standardowego algorytmu klasyfikacji.
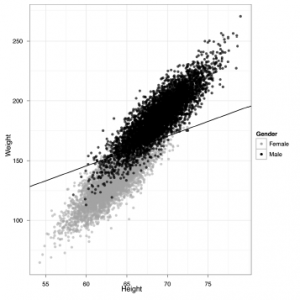
Narysowana przez nas linia ma bardzo fantazyjnie brzmiącą nazwę: „oddzielająca hiperpłaszczyzna”. Jest to „oddzielająca” hiperpłaszczyzna, ponieważ dzieli dane na dwie grupy: z jednej strony zgadujesz, że ktoś jest kobietą, biorąc pod uwagę jej wzrost i wagę, az drugiej strony zgadujesz, że jest mężczyzną. To całkiem dobry sposób na zgadywanie; dla tego zestawu danych masz rację przez około 92% czasu. Naszym zdaniem nie jest to złe działanie, gdy używasz tylko najprostszego modelu klasyfikacji, który ma tylko wysokości i wagi jako dane wejściowe do algorytmu prognozowania. W naszych prawdziwych zadaniach związanych z klasyfikacją często mamy dziesiątki, setki, a nawet tysiące danych wejściowych do wykorzystania w przewidywaniu klas. Z tym zestawem danych zdarza się szczególnie łatwo pracować i dlatego zaczęliśmy od niego. To koniec tego rozdziału. Jako zwiastun, który Cię ekscytuje w następnym rozdziale, pokażemy Ci kod R, który wygenerował prognozy, które właśnie zobaczyłeś. Jak widać, nie potrzebujesz prawie żadnego kodu, aby uzyskać dość imponujące wyniki.
heights.weights <- transform(heights.weights, Male = ifelse(Gender == ‘Male’, 1, 0))
logit.model <- glm(Male ~ Height + Weight, data = heights.weights,
family = binomial(link = ‘logit’))
ggplot(heights.weights, aes(x = Weight, y = Height, color = Gender)) +
geom_point() +
stat_abline(intercept = – coef(logit.model)[1] / coef(logit.model)[2],
slope = – coef(logit.model)[3] / coef(logit.model)[2],
geom = ‘abline’,
color = ‘black’)
W następnej części pokażemy dokładniej, jak budujesz własne klasyfikatory za pomocą gotowych narzędzi do uczenia maszynowego.