Miesiąc: maj 2020

Możesz pobrać R ze strony internetowej Comprehensive R Archive Network (CRAN). CRAN od czasu do czasu aktualizuje proces instalacji.. CRAN udostępnia instrukcje na stronie internetowej, jeśli proces się zmienił. Rozpocznij proces pobierania, przechodząc do strony internetowej http://cran.r-project.org. Na stronie internetowej znajdują się łącza do bieżących wersji systemów Windows, OS X i Linux okna otwierania. Wybierz odpowiedni link.

Windows

Na stronie, która otwiera się za pomocą linku Windows, wybierz bazę linków, która jest linkiem górnym. W następnym oknie kliknij link pobierania dla danej wersji systemu Windows. Jeśli wersja R nie została jeszcze zainstalowana na komputerze, program pobierający utworzy folder domyślny w folderze Dokumenty, w którym będą przechowywane pliki R. Jeśli nie ma powodu, aby zmieniać nazwę lub lokalizację folderu, zaakceptuj wartość domyślną. R rozpocznie pobieranie. Po zakończeniu pobierania programu znajdź pobrany plik w systemie plików. Pliki do pobrania są umieszczane w C: // Users / User_folder / Downloads, gdzie User_folder to folder użytkownika, chyba że wcześniej określono inny folder podczas instalacji. Kliknij pobrany plik, który jest plikiem instalacyjnym .exe .Może pojawić się pytanie o bezpieczeństwo programu. Program instalacyjny jest bezpieczny, więc uruchom go. Otworzy się kreator instalacji. Proces instalacji przechodzi przez kilka stron. Na pierwszej stronie przeczytaj OGÓLNĄ LICENCJĘ PUBLICZNĄ GNU; następnie kliknij Dalej. W przypadku pozostałych stron akceptacja ustawień domyślnych na każdej stronie jest w porządku, więc kliknij Dalej na każdej stronie. Na stronie dodatkowych opcji kliknij przycisk Dalej, a program rozpocznie instalację. Po zakończeniu instalacji kliknij przycisk Zakończ, aby zakończyć instalację. Program i 30 pakietów podstawowych są teraz zainstalowane. Ikona R pojawi się na pulpit komputera i, dla Windows 10. Aby uruchomić R, kliknij ikonę lub urok.

OS X

Na stronie, która otwiera się z linku OS X, najpierw przeczytaj sekcję R dla Mac OS X. Projekt R doradza sprawdzenie plików pod kątem wirusów i innych problemów. W obszarze Pliki: dostępne są dwie opcje pakietów: bieżąca wersja i najnowsza wersja. Wybranie bieżącej wersji spowoduje pobranie obu pakietów. Po zakończeniu pobierania pakietów otwórz okno pobierania na pasku ikon (żółte i brązowe pole) lub folder pobierania pod nazwą użytkownika w Finderze. Wybierz wersję R w polu pobierania. Otwarcie wersji otworzy instalatora. Po otwarciu instalatora kliknij przycisk Kontynuuj, aby przejść do następnej strony instalatora. Przeczytaj wiadomość z CRAN; następnie kliknij Kontynuuj. Ponownie przeczytaj wiadomość z CRAN; następnie kliknij Kontynuuj. Na następnej stronie znajdziesz licencję. Po przeczytaniu licencji kliknij opcję Zgadzam się, aby pobrać R. Na następnej stronie wybierz jedną z opcji; następnie kliknij Kontynuuj.

(Przycisk Kontynuuj nie zaświeci się, dopóki nie zostanie dokonany wybór.) Na następnej stronie wybierz Zainstaluj. Program instalacyjny poprosi o hasło. Po wprowadzeniu hasła rozpocznie się instalacja. Po zakończeniu instalacji kliknij Zamknij. R będzie teraz w folderze aplikacji i na stacji dokującej, a 30 podstawowych pakietów zostanie załadowanych. Wybierz R w doku lub w folderze aplikacji, aby uruchomić R.

Linux

W witrynie CRAN, CRAN zapewnia kod źródłowy R dla dystrybucji Linuksa Debian, Red Hat, Suse i Ubuntu. Deweloperzy twierdzą, że R jest dostępny za pośrednictwem systemu zarządzania pakietami dla większości dystrybucji Linuksa. Jeśli wersja R wiersza poleceń nie jest dostępna przy użyciu systemu zarządzania pakietami, opcjonalnie można zainstalować R bezpośrednio z terminala. Na stronie http://cran.r-project.org/ bin / linux / Distribution, gdzie dystrybucją jest Debian, Suse lub Ubuntu, instrukcje instalacji R można znaleźć w wierszu poleceń terminalu w plikach ReadMe. W przypadku Red Hat http://cran.r-project.org/bin/linux/redhat nie ma pliku ReadMe. Postępuj zgodnie z instrukcjami na stronie CRAN, aby zainstalować R dla Red Hat. Po zainstalowaniu R wiersz poleceń R będzie dostępny po wpisaniu R w oknie terminala.

Ale nie musimy jeszcze całkowicie rezygnować z tego zestawu danych. Chociaż nie udało nam się zbudować narzędzia, które przewiduje rangi na podstawie tekstów, możemy spróbować zrobić coś prostszego i sprawdzić, czy możemy przewidzieć, czy książka pojawi się w pierwszej 50. Aby to zrobić, zmienimy problem regresji na problem klasyfikacji. Zamiast przewidywać jedną z nieskończenie wielu możliwych stopni, przechodzimy do prostego kategorycznego osądu: czy ta książka znajduje się w pierwszej 50, czy nie?

Ponieważ to rozróżnienie jest o wiele szersze i prostsze, możemy mieć nadzieję, że łatwiej będzie wydobyć sygnał z naszego małego zestawu danych. Na początek dodajmy etykiety klas do naszego zestawu danych:

y <- rep (c (1, 0), każdy = 50)

W tym przypadku zastosowaliśmy kodowanie pozorne 0/1 omówione wcześniej, gdzie 1 oznacza, że ​​książka znajduje się w pierwszej 50, a 0 oznacza, że ​​książka nie znajduje się w pierwszej 50. Po wprowadzeniu tego kodu, możemy użyć algorytmu klasyfikacji regresji logistycznej,  aby przewidzieć obecność na liście 50 najlepszych książek. Regresja logistyczna jest w gruncie rzeczy regresją, w której przewiduje się prawdopodobieństwo, że element należy do jednej z dwóch kategorii. Ponieważ prawdopodobieństwa są zawsze między 0 a 1, możemy ustawić próg na 0,5, aby skonstruować algorytm klasyfikacji. Poza faktem, że wyniki wynoszą od 0 do 1, regresja logistyczna zachowuje się zasadniczo identycznie jak regresja liniowa. Jedyna różnica polega na tym, że musisz progować wyjścia, aby uzyskać prognozy klas. Przejdziemy przez ten próg, gdy pokażemy, jak łatwo dopasować regresję logistyczną w R. Na początek dopasujemy regresję logistyczną do całego zestawu danych, abyś mógł zobaczyć, jak to jest gotowe:

regularized.fit <- glmnet (x, y, family = ‘binomial’)

Jedyną różnicą między tym wezwaniem do glmnet a wezwaniem, które wykonaliśmy wcześniej w celu wykonania regresji liniowej, jest to, że ustawiamy dodatkowy parametr, family, która kontroluje rodzaj błędów, których można się spodziewać podczas prognozowania. Nie omówiliśmy tego wcześniej, ale regresja liniowa zakłada, że ​​widoczne błędy mają rozkład Gaussa, podczas gdy regresja logistyczna zakłada, że ​​błędy są rozkładane dwumianowo. Nie omawiamy szczegółów rozkładu dwumianowego, ale powinieneś wiedzieć, że jest to statystyczny rozkład danych, które uzyskasz po rzucie monetą. Z tego powodu rozkład dwumianowy powoduje błędy, które wszystkie są zerami lub zerami, co oczywiście jest potrzebne do klasyfikacji. Aby to rozwinąć, pokażmy trzy połączenia, które możesz wykonać w glmnet:

regularized.fit <- glmnet (x, y)

regularized.fit <- glmnet (x, y, family = ‘gaussian’)

regularized.fit <- glmnet (x, y, family = ‘binomial’)

Pierwsze wezwanie jest tym, które wykonaliśmy wcześniej w celu przeprowadzenia regresji liniowej. Drugie wywołanie jest w rzeczywistości równoważne pierwszemu wywołaniu, z tą różnicą, że wyraźnie podaliśmy domyślną wartość parametru rodziny, który jest automatycznie ustawiany na „gaussowski”. Trzecie połączenie to sposób przeprowadzania regresji logistycznej. Jak widać, zmiana analizy z regresji liniowej na regresję logistyczną to tylko kwestia zmiany rodziny błędów. Po dopasowaniu regresji logistycznej do całego zestawu danych, zobaczmy, jak wyglądają prognozy z naszego modelu za pomocą funkcji predict:

predict (regularized.fit, newx = x, s = 0,001)

# 1 4.884576

# 2 6,281354

# 3 4.892129

…

# 98 -5,958003

# 99 -5,677161

# 100 -4,956271

Jak widać, dane wyjściowe zawierają zarówno wartości dodatnie, jak i ujemne, mimo że mamy nadzieję uzyskać prognozy równe 0 lub 1. Są dwie rzeczy, które możemy zrobić z tymi surowymi prognozami. Pierwszym z nich jest przekroczenie progu 0 i wykonanie prognoz 0/1 za pomocą funkcji ifelse:

ifelse (przewidywanie (regularized.fit, newx = x, s = 0,001)> 0, 1, 0)

# 1 1

# 2 1

# 3 1

…

# 98 0

# 99 0

# 100 0

Drugi polega na przekształceniu tych surowych prognoz w prawdopodobieństwa, które możemy łatwiej zinterpretować – choć musielibyśmy ponownie wykonać progowanie na poziomie 0,5, aby uzyskać wygenerowane wcześniej prognozy 0/1. Aby przekonwertować surowe prognozy regresji logistycznej na prawdopodobieństwa, użyjemy funkcji inv.logit z pakietu rozruchowego:

library(‘boot’)

inv.logit(predict(regularized.fit, newx = x, s = 0.001))

#1 0.992494427

#2 0.998132627

#3 0.992550485

…

#98 0.002578403

#99 0.003411583

#100 0.006989922

Jeśli chcesz poznać szczegóły dotyczące działania inv.logit, zalecamy zapoznanie się z kodem źródłowym tej funkcji, aby dowiedzieć się, jaką matematyczną transformację oblicza. Dla naszych celów chcemy tylko, abyś zrozumiał, że regresja logistyczna oczekuje, że jej dane wyjściowe zostaną przekształcone przez funkcję odwrotnego logitu, zanim będziesz mógł wygenerować prawdopodobieństwa jako dane wyjściowe. Z tego powodu regresja logistyczna jest często nazywana modelem logit. Niezależnie od tego, w jaki sposób zdecydujesz się przekształcić nieprzetworzone dane wyjściowe z regresji logistycznej, tak naprawdę ważne jest to, że regresja logistyczna zapewnia narzędzie, które dokonuje klasyfikacji równie łatwo, jak przeprowadziliśmy regresję liniową w rozdziale 5. Spróbujmy więc użyć regresji logistycznej, aby zobaczyć, jak więc możemy zaklasyfikować książki do 50 najlepszych lub poniżej. Jak zauważysz, kod do wykonania tego jest zasadniczo identyczny z kodem, który użyliśmy wcześniej do dopasowania naszego modelu przewidywania rangi za pomocą regresji liniowej:

set.seed(1)

performance <- data.frame()

for (i in 1:250)

{

indices <- sample(1:100, 80)

training.x <- x[indices, ]

training.y <- y[indices]

test.x <- x[-indices, ]

test.y <- y[-indices]

for (lambda in c(0.0001, 0.001, 0.0025, 0.005, 0.01, 0.025, 0.5, 0.1))

{

glm.fit <- glmnet(training.x, training.y, family = ‘binomial’)

predicted.y <- ifelse(predict(glm.fit, test.x, s = lambda) > 0, 1, 0)

error.rate <- mean(predicted.y != test.y)

performance <- rbind(performance,

data.frame(Lambda = lambda,

Iteration = i,

ErrorRate = error.rate))

}

}

Zmiany algorytmiczne w tym fragmencie kodu w stosunku do tego, którego użyliśmy do regresji liniowej, są nieliczne: (1) wywołania glmnet, w których do regresji logistycznej używamy parametru rodziny błędów dwumianowych; (2) etap progowania, który daje prognozy 0/1 na podstawie surowych prognoz logistycznych; oraz (3) wykorzystanie wskaźników błędów zamiast RMSE jako naszej miary wydajności modelu. Kolejną zmianą, którą możesz zauważyć, jest to, że zdecydowaliśmy się wykonać 250 podziałów danych zamiast 50, abyśmy mogli lepiej poznać nasz średni poziom błędu dla każdego ustawienia lambda. Zrobiliśmy to, ponieważ wskaźniki błędów są bardzo zbliżone do 50%, i chcieliśmy potwierdzić, że naprawdę robimy coś lepszego niż przypadek przy prognozowaniu. Aby ten zwiększony podział był bardziej wydajny, odwróciliśmy kolejność pętli podziału i lambda, aby nie powtarzać podziału dla każdej pojedynczej wartości lambda. To oszczędza dużo czasu i służy jako przypomnienie, że pisanie efektywnego kodu uczenia maszynowego wymaga zachowywania się jak dobry programista, któremu zależy na pisaniu wydajnego kodu. Jesteśmy jednak bardziej zainteresowani naszą wydajnością w tym zbiorze danych, więc zróbmy wykres naszego poziomu błędów podczas przeglądania wartości lambda:

ggplot(performance, aes(x = Lambda, y = ErrorRate)) +

stat_summary(fun.data = ‘mean_cl_boot’, geom = ‘errorbar’) +

stat_summary(fun.data = ‘mean_cl_boot’, geom = ‘point’) +

scale_x_log10()

Wyniki mówią nam, że odnieśliśmy prawdziwy sukces, zastępując regresję klasyfikacją. W przypadku niskich wartości lambda jesteśmy w stanie uzyskać wyniki lepsze niż przypadkowe, przewidując, czy książka znajdzie się w pierwszej 50, co jest ulgą. Chociaż danych tych było po prostu za mało, aby zmieścić się w wyrafinowanej regresji przewidywania rang, okazuje się, że są wystarczająco duże, aby zmieścić się w znacznie prostszym binarnym rozróżnieniu, które dzieli książki na 50 najlepszych i poniżej. I to jest ogólna lekcja, na której zamkniemy ten rozdział: czasem prostsze rzeczy są lepsze. Regulararyzacja zmusza nas do korzystania z prostszych modeli, aby uzyskać wyższą wydajność naszych danych testowych. A przejście z modelu regresji na model klasyfikacji może dać znacznie lepszą wydajność, ponieważ wymagania dotyczące binarnego rozróżnienia są ogólnie znacznie słabsze niż wymagania dotyczące bezpośredniego przewidywania rang.

Część I wprowadza Cię w podstawy języka R. Aby użyć R, musisz najpierw pobrać program z Internetu. Opisuje, jak zainstalować R w systemach operacyjnych Windows, OS X i Linux. Opisuje również sposób instalowania i aktualizowania pakietów oraz aktualizowania R i używania R w systemie plików. Po zainstalowaniu i otwarciu R pojawi się monit R i niewiele więcej. Przedstawia części R (obiekty, operatory i przypisania), monit R i przykład użycia R jako kalkulatora z monitu R. Pokazuje, jak przypisywać nazwy do wyrażeń w celu utworzenia obiektów R i opisuje dwie funkcje: ls() do wyświetlania obiektów w obszarze roboczym i rm() do usuwania obiektów z obszaru roboczego. Następnie omawia operatory działające na obiektach i wyrażeniach: operatory logiczne, arytmetyczne, macierzowe, relacyjne i indeksujące, a także kilka innych operatorów specjalnych

Walidacja krzyżowa i legalizacja to zarówno potężne narzędzia, które pozwalają nam korzystać ze złożonych modeli, które mogą naśladować bardzo skomplikowane wzorce w naszych danych bez nadmiernego dopasowania. Jednym z najciekawszych przypadków, w których możemy zastosować regularyzację, jest użycie tekstu do przewidywania ciągłego wyniku; na przykład możemy spróbować przewidzieć, jak niestabilna będzie akcja na podstawie zgłoszeń z pierwszej oferty publicznej. Kiedy używamy tekstu jako danych wejściowych dla problemu regresji, prawie zawsze mamy znacznie więcej danych wejściowych (słów) niż obserwacji (dokumentów). Jeśli mamy więcej obserwacji niż 1-gram (pojedyncze słowa), możemy po prostu rozważyć 2-gramy (pary słów) lub 3-gramy (trojaczki słów), dopóki nie otrzymamy więcej n-gramów niż dokumentów. Ponieważ nasz zestaw danych ma więcej kolumn niż wierszy, nieregularna regresja liniowa zawsze spowoduje powstanie modelu overfit. Z tego powodu musimy zastosować jakąś formę regularyzacji, aby uzyskać jakiekolwiek znaczące wyniki. Aby dać ci poczucie tego problemu, przeanalizujemy proste studium przypadku, w którym staramy się przewidzieć względną popularność najlepiej sprzedających się książek, które O’Reilly kiedykolwiek opublikował, wykorzystując tylko ich opisy ich tylne okładki jako dane wejściowe. Aby przekształcić te opisy tekstowe w użyteczny zestaw danych wejściowych, przekonwertujemy opisy każdej książki na wektor liczenia słów, abyśmy mogli zobaczyć, jak często w każdym opisie występują słowa takie jak „the” i „Perl”. Wyniki naszej analizy będą teoretycznie listą słów w opisie książki, które przewidują wysoką sprzedaż. Oczywiście zawsze jest możliwe, że zadania przewidywania po prostu nie da się zrealizować. Może to wynikać z przypisywania przez model wysokich współczynników słowom zasadniczo arbitralnym. Oznacza to, że może być bardzo mało popularnych słów w opisach popularnych książek O’Reilly, ale ponieważ model tego nie wie, nadal będzie próbował dopasować dane i przypisać wartość niektórym słowom. Jednak w tym przypadku wyniki nie dostarczą żadnych nowych informacji na temat tego, co czyni te słowa użytecznymi. Ten problem nie pojawi się wyraźnie w tym przykładzie, ale bardzo ważne jest, aby o tym pamiętać podczas regresji tekstu. Na początek załaduj nasz nieprzetworzony zestaw danych i przekształć go w matrycę terminów dokumentu, używając pakietu tm, który wprowadziliśmy wcześniej:

ranks <- read.csv(‘data/oreilly.csv’, stringsAsFactors = FALSE)

library(‘tm’)

documents <- data.frame(Text = ranks$Long.Desc.)

row.names(documents) <- 1:nrow(documents)

corpus <- Corpus(DataframeSource(documents))

corpus <- tm_map(corpus, tolower)

corpus <- tm_map(corpus, stripWhitespace)

corpus <- tm_map(corpus, removeWords, stopwords(‘english’))

dtm <- DocumentTermMatrix(corpus)

Tutaj załadowaliśmy zestaw danych szeregów z pliku CSV, utworzyliśmy ramkę danych, która zawiera opisy książek w formacie, który rozumie tm, utworzyliśmy korpus z tej ramki danych, znormalizowaliśmy wielkość liter tekstu, usunięto białe znaki , usunęliśmy najczęstsze słowa w języku angielskim i zbudowaliśmy naszą matrycę terminów dokumentów. Po tych pracach zakończyliśmy wszystkie istotne transformacje, które musimy wprowadzić do naszych danych. Po ich zakończeniu możemy trochę manipulować naszymi zmiennymi, aby ułatwić opisanie naszego problemu z regresją w glmnet:

x <- as.matrix (dtm)

y <- rev (1: 100)

W tym miejscu przekonwertowaliśmy matrycę terminów dokumentów na prostą matrycę numeryczną, z którą łatwiej jest pracować. I zakodowaliśmy szeregi w odwrotnym kodowaniu, aby książka o najwyższym rankingu miała wartość y równą 100, a książka o najniższym rankingu miała wartość y równą 1. Robimy to, aby współczynniki, które przewidywały popularność książki są pozytywne, gdy sygnalizują wzrost popularności; gdybyśmy zamiast tego użyli surowych szeregów, współczynniki dla tych samych słów musiałyby być ujemne. Uważamy, że jest to mniej intuicyjne, chociaż nie ma istotnej różnicy między dwoma systemami kodowania. Na koniec, przed uruchomieniem naszej analizy regresji, musimy zainicjować losowe ziarno i załadować pakiet glmnet:

set.seed (1)

library („glmnet”)

Po zakończeniu prac konfiguracyjnych możemy zapętlić kilka możliwych wartości dla Lambda, aby zobaczyć, które dają najlepsze wyniki w przetrzymywanych danych. Ponieważ nie mamy dużo danych, dokonujemy tego podziału 50 razy dla każdej wartości Lambda, aby uzyskać lepsze poczucie dokładności, którą uzyskujemy z różnych poziomów regularyzacji. W poniższym kodzie ustawiliśmy wartość dla Lambda, podzieliliśmy dane na zestaw szkoleniowy i zestaw testowy 50 razy, a następnie oceniliśmy wydajność naszego modelu przy każdym podziale

performance <- data.frame()

for (lambda in c(0.1, 0.25, 0.5, 1, 2, 5))

{

for (i in 1:50)

{

indices <- sample(1:100, 80)

training.x <- x[indices, ]

training.y <- y[indices]

test.x <- x[-indices, ]

test.y <- y[-indices]

glm.fit <- glmnet(training.x, training.y)

predicted.y <- predict(glm.fit, test.x, s = lambda)

rmse <- sqrt(mean((predicted.y – test.y) ^ 2))

performance <- rbind(performance,

data.frame(Lambda = lambda,

Iteration = i,

RMSE = rmse))

}

}

Po obliczeniu wydajności modelu dla tych różnych wartości Lambda, możemy je porównać, aby zobaczyć, gdzie model najlepiej sobie radzi:

ggplot(performance, aes(x = Lambda, y = RMSE)) +

stat_summary(fun.data = ‘mean_cl_boot’, geom = ‘errorbar’) +

stat_summary(fun.data = ‘mean_cl_boot’, geom = ‘point’)

Niestety, spojrzenie na rysunek sugeruje, że jest to nasz pierwszy przykład nieudanej próby zastosowania metody statystycznej do danych.

Oczywiste jest, że model staje się coraz lepszy wraz z wyższymi wartościami Lambda, ale dzieje się to dokładnie wtedy, gdy model ogranicza się do niczego więcej niż przechwytywanie. W tym momencie nie używamy żadnych danych tekstowych. Krótko mówiąc, tutaj nie ma sygnału, że można znaleźć naszą regresję tekstu. Wszystko, co widzimy, okazuje się być hałasem, gdy testujesz model pod kątem wstrzymanych danych. Chociaż oznacza to, że nie mamy lepszego pomysłu na to, jak napisać opis tylnej okładki książki, aby upewnić się, że dobrze się sprzedaje, jest to cenna lekcja dla każdego, kto pracuje nad uczeniem maszynowym do przyswojenia: czasami po prostu nie ma sygnału w danych, z którymi pracujesz.

R to język programowania, który zapewnia użytkownikowi zaawansowane opcje analizy danych i grafiki. R jest zarówno elastyczny, jak i szeroki. Od zadań tak prostych jak dodawanie dwóch liczb do zadań tak skomplikowanych jak dopasowanie modelu ARIMA, R jest w stanie rozbić liczby. Naszym celem jest zapewnienie czytelnikowi podstawowej składni R. Często użytkownik R blokuje się, jeśli na przykład tryb jest nieprawidłowy lub test logiczny nie działa. Ponieważ pełne spektrum pakietów R wykorzystuje tę samą dość prostą składnię, dostarczymy  czytelnikowi niezbędnych informacji do odblokowania się i uruchomienia i utworzenia wszystkich funkcji R. Język R jest oparty na języku S, języku programowania wysokiego poziomu opracowanym głównie przez Richarda A. Beckera, Johna M. Chambersa i Allana R. Wilksa w laboratoriach AT&T w 1975 r. Wersja R języka najpierw stała się dostępna w 1993 r. i został opracowany przez Rossa Ihakę i Roberta Gentlemana z University of Auckland, Nowa Zelandia. R jest open source i jest projektem GNU. Jako kod typu open source, język R jest darmowy i jest ciągle ulepszany. Zespół podstawowy ds. Rozwoju R zajmuje się obecnie opracowywaniem. Pakiety dla określonych technik analizy są często dodawane. Większość użytkowników korzysta tylko z kilku pakietów. Chociaż dostępne są wersje R interfejsu GUI, omawiamy użycie R w wierszu polecenia

Część I obejmuje podstawy R. Opisujemy, jak pobrać i zainstalować R dla systemów operacyjnych Windows, Mac i Linux, a także jak pobierać pakiety. Ponieważ przechowywanie osobnych folderów dla różnych projektów jest bardzo przydatne, zawieramy instrukcje uruchamiania R z różnych folderów. Podaje także metody aktualizacji samego programu R. Wprowadza monit R, podajemy przykładowe obliczenia i opisujemy trzy części R – obiektów, operatorów i przypisań. Obejmuje przypisywanie nazw do obiektów, demonstruje funkcję ls(), która pozwala zobaczyć obiekty w folderze, i omawia operatory w R.

Część II opisuje obiekty R. Obiekty mają tryby, klasy i typy. Zawiera listę trybów i opisuje niektóre z nich. Pokazuje także różnice między trybami i typami. Omawia niektóre klasy.

Część III obejmuje funkcje. Rozpoczyna się od listy 30 domyślnych pakietów w języku R, a następnie zawiera instrukcje dotyczące korzystania z funkcji. Ponieważ wszystkie funkcje spakowane mają strony pomocy, zawiera instrukcje dotyczące dostępu do strony pomocy funkcji i korzystania z niej. Opisuje, jak utworzyć funkcję. Wyjaśnia, jak uruchomić funkcję – ze szczegółowym podejściem do listy argumentów.

Część IV koncentruje się na importowaniu i eksportowaniu danych w języku R oraz metodach tworzenia i manipulowania niektórymi obiektami. Opisuje kilka metod importowania danych, podaje szereg funkcji do tworzenia obiektów danych i omawia niektóre generatory liczb losowych. Podaje kilka metod eksportowania z R. Podaje szereg funkcji, które działają na obiektach – do wiązania obiektów razem, znajdowania cech opisowych obiektu, przypisywania właściwości do obiektu, agregowania obiektu w jakiś sposób, lub zastosować funkcje do części obiektu.

Część V obejmuje polecenia i funkcje warunkowania przepływu. Przedstawia instrukcje warunkowania przepływu, i  podaje ich przykłady. Opisuje dwie funkcje warunkowania przepływu i podaje przykłady.

Część VI omawia funkcje związane z formatowaniem i wyprowadzaniem danych wyjściowych, analizuje wyniki funkcji spakowanych i zawartość niektórych pakietów domyślnych oraz podaje kilka wskazówek dotyczących korzystania z R. Podaje niektóre funkcje zaokrąglania i niektóre funkcje do wyprowadzania z funkcji . Daje również niektóre funkcje, które różnią się w zależności od klasy obiektu, na którym działa funkcja, i które podsumowują wyniki funkcji, zarówno tekstowo, jak i wizualnie. Przedstawia zawartość bazy pakietów, statystyki i grafikę oraz rzut oka na zestawy danych, grDevices, metody i pakiety narzędzi. Opisuje, jak radzić sobie z niektórymi powszechnymi frustracjami w R. Więcej informacji na temat wyprowadzania z funkcji, plus przykład funkcji rekurencyjnej i porady dotyczące używania R.

Mówiliśmy o modelach zbyt złożonych, ale nigdy nie podaliśmy formalnej definicji złożoności. Jednym podejściem podczas pracy z regresją wielomianową byłoby stwierdzenie, że modele są bardziej złożone, gdy stopień jest większy; wielomian stopnia 2 jest na przykład bardziej złożony niż wielomian stopnia 1. Ale to ogólnie nie pomaga nam w regresji liniowej. Wykorzystamy więc alternatywną miarę złożoności: powiemy, że model jest skomplikowany, gdy współczynniki są duże. Na przykład powiedzielibyśmy, że model y ~ 5 * x + 2 jest bardziej skomplikowany niż model y ~ 3 * x + 2. Zgodnie z tą samą logiką powiemy, że model y ~ 1 * x ^ 2 + 1 * x + 1 jest bardziej skomplikowany niż model y ~ 1 * x + 1. Aby zastosować tę definicję w praktyce, możemy dopasować model za pomocą lm, a następnie zmierzyć jego złożoność poprzez zsumowanie wartości zwróconych przez cewkę:

lm.fit <- lm (y ~ x)

model.complexity <- sum (coef (lm.fit) ^ 2)

Tutaj wyliczyliśmy współczynniki przed ich zsumowaniem, aby nie wzajemnie się anulowały, gdy dodamy je wszystkie razem. Ten krok do kwadratu jest często nazywany normą L2. Alternatywnym podejściem do wyrównywania współczynników jest wzięcie zamiast tego bezwzględnej wartości współczynników; to drugie podejście nazywa się normą L1. Tutaj obliczamy dwa z nich w R:

lm.fit <- lm (y ~ x)

l2.model.complexity <- sum (coef (lm.fit) ^ 2)

l1.model.complexity <- sum (abs (coef (lm.fit)))

Te miary złożoności modelu mogą początkowo wydawać się dziwne, ale za chwilę przekonasz się, że naprawdę są pomocne, gdy próbujesz zapobiec nadmiernemu dopasowaniu. Powodem jest to, że możemy użyć tej miary złożoności, aby zmusić nasz model do uproszczenia podczas dopasowywania modelu. Wielki pomysł polega na tym, że kompromisowo dostosowujemy model tak, aby jak najlepiej pasował do danych treningowych, biorąc pod uwagę stopień złożoności modelu. To prowadzi nas do jednego z najbardziej krytycznych kryteriów decyzyjnych podczas modelowania danych: ponieważ dokonujemy kompromisu między dopasowaniem danych a złożonością modelu, ostatecznie wybieramy prostszy model, który pasuje gorzej, niż bardziej złożony model, który lepiej pasuje . Ten kompromis, który rozumiemy przez regularyzację, ostatecznie zapobiega nadmiernemu dopasowaniu, ograniczając naszemu modelowi dopasowanie hałasu w danych szkoleniowych, których używamy, aby go dopasować. Na razie porozmawiajmy o narzędziach, których możesz użyć do pracy z regularyzacją w R. W tym rozdziale zajmiemy się używaniem pakietu glmnet, który udostępnia funkcję o nazwie glmnet, która pasuje do modeli liniowych z wykorzystaniem regularyzacji. Aby zobaczyć, jak działa Glmnet, wróćmy jeszcze raz do naszych danych sinusoidalnych:

set.seed(1)

x <- seq(0, 1, by = 0.01)

y <- sin(2 * pi * x) + rnorm(length(x), 0, 0.1)

Aby użyć glmnet, musimy najpierw przekonwertować naszą wektorową kopię x na macierz za pomocą funkcji macierzy. Następnie wywołujemy glmnet w odwrotnej kolejności niż ta, której użyłbyś z lm i jego składnią ~ -operator:

x <- matrix(x)

library(‘glmnet’)

glmnet(x, y)

#Call: glmnet(x = x, y = y)

#

# Df %Dev Lambda

# [1,] 0 0.00000 0.542800

# [2,] 1 0.09991 0.494600

# [3,] 1 0.18290 0.450700

# [4,] 1 0.25170 0.410600

# [5,] 1 0.30890 0.374200

…

#[51,] 1 0.58840 0.005182

#[52,] 1 0.58840 0.004721

#[53,] 1 0.58850 0.004302

#[54,] 1 0.58850 0.003920

#[55,] 1 0.58850 0.003571

Kiedy wywołujesz glmnet w ten sposób, odzyskujesz cały zestaw możliwych regularyzacji regresji, o którą poprosiłeś ją. Na górze listy znajduje się najsilniejsza regularyzacja wykonana przez glmnet, a na dole listy jest najsłabsza obliczona normalizacja. W wynikach, które cytowaliśmy tutaj, pokazujemy pierwsze pięć wierszy i pięć ostatnich. Porozmawiajmy o interpretacji każdej kolumny wyniku dla tych 10 wierszy, które pokazaliśmy. Każdy wiersz wyniku zawiera trzy kolumny: (1) Df, (2)% Dev i (3) Lambda. Pierwsza kolumna, Df, mówi, ile współczynników w modelu skończyło się na niezerowych. Pamiętaj, że nie obejmuje to terminu przechwytywania, którego nie chcesz karać za jego rozmiar. Znajomość liczby niezerowych współczynników jest przydatna, ponieważ wiele osób chciałoby być w stanie stwierdzić, że tylko kilka danych wejściowych naprawdę ma znaczenie, i możemy to zapewnić bardziej pewnie, jeśli model działa dobrze, nawet gdy przypisuje zerową wagę wielu wejściom. Gdy większość danych wejściowych do modelu statystycznego ma przypisane zerowe współczynniki, mówimy, że model jest rzadki. Opracowywanie narzędzi do promowania rzadkości w modelach statystycznych jest głównym tematem we współczesnych badaniach nad uczeniem maszynowym. Druga kolumna,% Dev, jest zasadniczo R2 dla tego modelu. W górnym rzędzie wynosi 0%, ponieważ masz zerowy współczynnik dla jednej zmiennej wejściowej, a zatem nie możesz uzyskać lepszej wydajności niż zwykłe przechwytywanie. W dolnym rzędzie Dev wynosi 59%, co jest wartością, którą uzyskałbyś, używając lm bezpośrednio, ponieważ lm w ogóle nie dokonuje żadnej regularyzacji. Pomiędzy tymi dwiema skrajnościami regularyzacji modelu aż do przechwytywania i wcale nie regulowania, zobaczysz wartości dla Dev w zakresie od 9% do 58%. Ostatnia kolumna, Lambda, jest najważniejszą informacją dla kogoś, kto uczy się o regularyzacji. Lambda to parametr algorytmu regularyzacji, który kontroluje stopień złożoności dopasowanego modelu. Ponieważ kontroluje wartości, które ostatecznie uzyskasz dla głównych parametrów modelu, Lambda jest często nazywany hiperparametrem. Kiedy Lambda jest bardzo duża, bardzo karzesz swój model za to, że jest złożony, a ta penalizacja popycha wszystkie współczynniki w kierunku zera. Kiedy Lambda jest bardzo mała, wcale nie karasz za swój model. Na najdalszym końcu tego spektrum, w kierunku słabszej regularyzacji, możemy ustawić Lambdę na 0 i uzyskać wyniki takie jak te z nieregularnej regresji liniowej takiej, jaką pasowalibyśmy przy użyciu lm. Ale generalnie gdzieś w tych dwóch skrajnościach możemy znaleźć ustawienie dla Lambdy, które daje najlepszy możliwy model. Jak znaleźć tę wartość dla Lambda? Tutaj stosujemy walidację krzyżową jako część procesu pracy z regularyzacją. Zamiast bawić się stopniem regresji wielomianowej, możemy ustawić stopień na wysoką wartość, na przykład 10, już na początku. Następnie dopasujemy model z różnymi wartościami dla Lambda na zestawie treningowym i zobaczymy, jak działa na wyciągniętym zestawie testowym. Po zrobieniu tego dla wielu wartości Lambda, będziemy mogli zobaczyć, która wartość Lambda daje nam najlepszą wydajność na danych testowych. Absolutnie musisz ocenić jakość swojej regularyzacji na danych testowych. Zwiększenie siły regularyzacji może tylko pogorszyć Twoją wydajność w danych treningowych, więc dosłownie zero informacji możesz nauczyć się patrząc na swoją wydajność w danych treningowych. Mając to na uwadze, przejdźmy teraz do przykładu. Tak jak poprzednio, skonfigurujemy nasze dane i podzielimy je na zestaw szkoleniowy i testowy:

set.seed(1)

x <- seq(0, 1, by = 0.01)

y <- sin(2 * pi * x) + rnorm(length(x), 0, 0.1)

n <- length(x)

indices <- sort(sample(1:n, round(0.5 * n)))

training.x <- x[indices]

training.y <- y[indices]

test.x <- x[-indices]

test.y <- y[-indices]

df <- data.frame(X = x, Y = y)

training.df <- data.frame(X = training.x, Y = training.y)

test.df <- data.frame(X = test.x, Y = test.y)

rmse <- function(y, h)

{

return(sqrt(mean((y – h) ^ 2)))

}

Ale tym razem zapętlimy wartości Lambda zamiast stopni. Na szczęście nie musimy za każdym razem modernizować modelu, ponieważ glmnet przechowuje dopasowany model dla wielu wartości Lambda po jednym kroku dopasowania.

library(‘glmnet’)

glmnet.fit <- with(training.df, glmnet(poly(X, degree = 10), Y))

lambdas <- glmnet.fit$lambda

performance <- data.frame()

for (lambda in lambdas)

{

performance <- rbind(performance,

data.frame(Lambda = lambda,

RMSE = rmse(test.y, with(test.df, predict(glmnet.fit, poly(X,

degree = 10), s = lambda)))))

}

Po obliczeniu wydajności modelu dla różnych wartości Lambda, możemy skonstruować wykres, aby zobaczyć, gdzie w zakresie testowanych lambd możemy uzyskać najlepszą wydajność na nowych danych:

ggplot(performance, aes(x = Lambda, y = RMSE)) +

geom_point() +

geom_line()

Patrząc na rysunek ,

wygląda na to, że uzyskujemy najlepszą możliwą wydajność z Lambda blisko 0,05. Aby dopasować model do pełnych danych, możemy wybrać tę wartość i wyszkolić nasz model na całym zestawie danych. Tutaj robimy tylko to:

best.lambda <- with(performance, Lambda[which(RMSE == min(RMSE))])

glmnet.fit <- with(df, glmnet(poly(X, degree = 10), Y))

Po dopasowaniu naszego ostatecznego modelu do całego zestawu danych, możemy użyć coef do zbadania struktury naszego znormalizowanego modelu:

coef(glmnet.fit, s = best.lambda)

#11 x 1 sparse Matrix of class “dgCMatrix”

# 1

#(Intercept) 0.0101667

#1 -5.2132586

#2 0.0000000

#3 4.1759498

#4 0.0000000

#5 -0.4643476

#6 0.0000000

#7 0.0000000

#8 0.0000000

#9 0.0000000

#10 0.0000000

Jak widać z tej tabeli, ostatecznie używamy tylko 3 niezerowych współczynników, mimo że model ma możliwość użycia 10. Wybór prostszego modelu takiego, nawet jeśli możliwe są bardziej skomplikowane modele, jest główną strategią za regularyzacją. A dzięki regularyzacji w naszym zestawie narzędzi możemy w dużym stopniu zastosować regresję wielomianową i nadal powstrzymywać się od przeładowywania danych. Po wprowadzeniu podstawowych pomysłów na regularyzację, spójrzmy na praktyczne zastosowanie w studium przypadku

Zanim będziemy w stanie zapobiec nadmiernemu dopasowaniu, musimy nadać temu terminowi rygorystyczne znaczenie. Rozmawialiśmy o tym, że model jest nadmiernie dopasowany, gdy pasuje do części szumu w zestawie danych, a nie do prawdziwego podstawowego sygnału. Ale jeśli nie znamy prawdy, to jak możemy powiedzieć, że oddalamy się od niej, a nie bliżej? Sztuką jest wyjaśnienie, co rozumiemy przez prawdę. Dla naszych celów model predykcyjny jest bliski prawdy, gdy jego prognozy dotyczące przyszłych danych są dokładne. Ale oczywiście nie mamy dostępu do przyszłych danych; mamy tylko dane z przeszłości. Na szczęście możemy symulować, jak by to było mieć dostęp do danych w przyszłości, dzieląc nasze dane z przeszłości na dwie części. Prosty przykład wyjaśni naszą ogólną strategię: wyobraź sobie, że próbujemy zbudować model do przewidywania temperatur w przyszłości. Mamy dane za okres od stycznia do czerwca i chcemy dokonać prognoz na lipiec. Możemy sprawdzić, który z naszych modeli jest najlepszy, dopasowując je do danych od stycznia do maja, a następnie testując te modele na danych z czerwca. Gdybyśmy zrobili ten krok dopasowania modelu w maju, naprawdę testowalibyśmy nasz model na podstawie przyszłych danych. Możemy więc wykorzystać tę strategię dzielenia danych, aby wykonać całkowicie realistyczną symulację doświadczeń związanych z testowaniem naszego modelu na niewidzialnych danych. U podstaw weryfikacji krzyżowej leży po prostu nasza zdolność do symulowania testowania naszego modelu na przyszłych danych, ignorując część naszych danych historycznych podczas procesu dopasowania modelu. Jeśli przejrzałeś sprawy w rozdziałach 3 i 4, pamiętasz, że właśnie to zrobiliśmy. W każdym przypadku dzielimy nasze dane, aby trenować i testować nasze modele klasyfikacji i rankingu. Prawdopodobnie jest to po prostu instancja metody naukowej, której wszyscy uczono nas jako dzieci: (1) formułuje hipotezę, (2) zbiera dane i (3) ją testuje. Jest tylko odrobina sztuczki, ponieważ nie formułujemy hipotezy na podstawie istniejących danych, a następnie wychodzimy i zbieramy więcej danych. Zamiast tego ignorujemy część naszych danych podczas formułowania naszych hipotez, abyśmy mogli magicznie odkryć brakujące dane, gdy przyjdzie czas na przetestowanie naszych prognoz. Zanim skorzystamy z weryfikacji krzyżowej w złożonej aplikacji, przejrzyjmy zabawkowy przykład, w jaki sposób możemy użyć weryfikacji krzyżowej, aby wybrać stopień regresji wielomianowej dla danych fali sinusoidalnej, które mieliśmy wcześniej. Najpierw odtworzymy nasze dane fali sinusoidalnej:

set.seed(1)

x <- seq(0, 1, by = 0.01)

y <- sin(2 * pi * x) + rnorm(length(x), 0, 0.1)

Następnie musimy podzielić nasze dane na dwie części: zestaw szkoleniowy, którego użyjemy, aby dopasować do naszego modelu oraz zestaw testowy, którego użyjemy do przetestowania wydajności modelu. Zestaw treningowy można traktować jako dane z przeszłości, natomiast zestaw testowy to dane przyszłe. W tym przykładzie podzielimy dane dokładnie na pół. W przypadku niektórych aplikacji lepiej jest użyć więcej danych dla zestawu treningowego (powiedzmy, 80%) i mniej danych dla zestawu testowego (powiedzmy, 20%), ponieważ im więcej danych masz podczas dopasowywania modelu, tym lepiej dopasowany model będzie miał tendencję być. Jak zawsze twój przebieg będzie się różnił, więc eksperymentuj w obliczu jakiegokolwiek problemu w świecie rzeczywistym. Zróbmy podział, a następnie porozmawiajmy o szczegółach:

n <- length(x)

indices <- sort(sample(1:n, round(0.5 * n)))

training.x <- x[indices]

training.y <- y[indices]

test.x <- x[-indices]

test.y <- y[-indices]

training.df <- data.frame(X = training.x, Y = training.y)

test.df <- data.frame(X = test.x, Y = test.y)

Tutaj skonstruowaliśmy losowy wektor wskaźników, który definiuje zestaw treningowy. Dobrym pomysłem jest zawsze losowe dzielenie danych podczas dzielenia zestawu treningowego / zestawu testowego, ponieważ nie chcesz, aby zestaw treningowy i zestaw testowy systematycznie się różniły – tak może się zdarzyć, na przykład, jeśli wstawisz tylko najmniejsze wartości dla x do zestawu treningowego, a największe wartości do zestawu testowego. Losowość wynika z zastosowania funkcji próbki R, która generuje losową próbkę z danego wektora. W naszym przypadku podajemy wektor liczb całkowitych, od 1 do n, i próbkujemy ich połowę. Po ustaleniu wartości indeksów oddzielamy zestawy szkoleniowe i testowe, stosując reguły indeksowania wektorowego R. Na koniec tworzymy ramkę danych do przechowywania danych, ponieważ łatwiej jest pracować z lm podczas korzystania z ramek danych. Po podzieleniu danych na zestaw szkoleniowy i testowy chcemy przetestować różne stopnie pod kątem regresji wielomianowej, aby zobaczyć, która z nich działa najlepiej. Użyjemy RMSE do pomiaru naszej wydajności. Aby nasz kod był nieco czytelniejszy, stworzymy specjalną funkcję rmse:

rmse <- function(y, h)

{

return(sqrt(mean((y – h) ^ 2)))

}

Then we’ll loop over a set of polynomial degrees, which are the integers between

1 and 12:

performance <- data.frame()

for (d in 1:12)

{

poly.fit <- lm(Y ~ poly(X, degree = d), data = training.df)

performance <- rbind(performance,

data.frame(Degree = d,

Data = ‘Training’,

RMSE = rmse(training.y, predict(poly.fit))))

performance <- rbind(performance,

data.frame(Degree = d,

Data = ‘Test’,

RMSE = rmse(test.y, predict(poly.fit,

newdata = test.df))))

}

Podczas każdej iteracji tej pętli dopasowujemy regresję wielomianową stopnia d do danych w training.df, a następnie oceniamy jej wydajność zarówno na training.df, jak i test.df. Przechowujemy wyniki w ramce danych, abyśmy mogli szybko analizować wyniki po zakończeniu pętli. W tym przypadku używamy nieco innej techniki konstruowania ramek danych niż w przeszłości. Zaczynamy od przypisania pustej ramki danych zmiennej wydajności, do której następnie iteracyjnie dodajemy wiersze za pomocą funkcji rbind. Jak wspomnieliśmy wcześniej, często istnieje wiele sposobów wykonania tego samego zadania manipulacji danymi w języku R, ale rzadko pętla tego rodzaju jest najbardziej wydajna. Używamy go tutaj, ponieważ dane są dość małe i pozwala to na wyraźniejsze zrozumienie procesu algorytmu, ale pamiętaj o tym, pisząc własne testy wzajemnej weryfikacji. Po zakończeniu wykonywania pętli możemy wykreślić wydajność modeli regresji wielomianowej dla wszystkich stopni, których próbowaliśmy:

ggplot(performance, aes(x = Degree, y = RMSE, linetype = Data)) +

geom_point() +

geom_line()

Wynik pokazano poniżej

wyjaśnia, że ​​użycie stopnia pośrodku zakresu, z którym eksperymentowaliśmy, zapewnia nam najlepszą wydajność naszych danych testowych. Gdy stopień jest tak niski jak 1 lub 2, model nie rejestruje prawdziwego wzorca w danych i widzimy bardzo słabą wydajność predykcyjną zarówno danych treningowych, jak i testowych. Gdy model nie jest wystarczająco skomplikowany, aby zmieścić nawet dane treningowe, nazywamy to niedopasowaniem. Na przeciwległym końcu naszego wykresu w pobliżu stopni 11 i 12 widzimy, że prognozy dla modelu znów zaczynają się pogarszać na danych testowych. Jest tak, ponieważ model staje się zbyt złożony i hałaśliwy, i pasuje do dziwactw w danych treningowych, których nie ma w danych testowych. Kiedy zaczynasz modelować dziwactwa losowe w swoich danych, nazywamy to nadmiernym dopasowaniem. Innym sposobem myślenia o nadmiernym dopasowaniu jest zauważenie, że nasza wydajność na zestawie treningowym i zestawie testowym zaczyna się różnić w miarę przesuwania się w prawo na powyższym rysunku: poziom błędu zestawu treningowego spada, ale wydajność zestawu testowego zaczyna rosnąć . Nasz model nie uogólnia na dane wykraczające poza określone punkty wyszkolonw na – i to sprawia, że ​​się przepełnia. Na szczęście nasza fabuła informuje nas, jak ustawić stopień regresji, aby uzyskać najlepszą wydajność z naszego modelu. Ten punkt pośredni, który nie jest ani niedopasowany, ani nadmierny, byłby bardzo trudny do wykrycia bez zastosowania weryfikacji krzyżowej. Po krótkim objaśnieniu, w jaki sposób możemy zastosować walidację krzyżową w przypadku nadmiernego dopasowania, przejdziemy do omówienia innego podejścia do zapobiegania nadmiernemu dopasowaniu, które nazywa się regularyzacją. Normalizacja różni się znacznie od weryfikacji krzyżowej w duchu, nawet jeśli ostatecznie zastosujemy weryfikację krzyżową, aby pokazać, że regularyzacja jest w stanie zapobiec nadmiernemu dopasowaniu. Będziemy także musieli użyć weryfikacji krzyżowej, aby skalibrować nasz algorytm regularyzacji, więc te dwa pomysły ostatecznie zostaną ściśle powiązane.

Mając na uwadze nasze wcześniejsze zastrzeżenia, zacznijmy od regresji wielomianowej w R, która jest zaimplementowana w funkcji poly. Najłatwiejszym sposobem, aby zobaczyć, jak działa poly, jest zbudowanie z prostego przykładu i pokazanie, co się dzieje, gdy dajemy naszemu modelowi bardziej ekspresyjną moc naśladowania struktury naszych danych. Użyjemy fali sinusoidalnej, aby utworzyć zestaw danych, w którym związek między x i y nigdy nie może być opisany prostą linią.

set.seed(1)

x <- seq(0, 1, by = 0.01)

y <- sin(2 * pi * x) + rnorm(length(x), 0, 0.1)

df <- data.frame(X = x, Y = y)

ggplot(df, aes(x = X, y = Y)) +

geom_point()

Wystarczy spojrzeć na te dane, które pokazano na rysunku,

jasne jest, że użycie prostego modelu regresji liniowej nie zadziała. Ale uruchommy prosty model liniowy i zobaczmy, jak on działa.

summary(lm(Y ~ X, data = df))

#Call:

#lm(formula = Y ~ X, data = df)

#

#Residuals:

# Min 1Q Median 3Q Max

#-1.00376 -0.41253 -0.00409 0.40664 0.85874

#

#Coefficients:

# Estimate Std. Error t value Pr(>|t|)

#(Intercept) 0.94111 0.09057 10.39 <2e-16 ***

#X -1.86189 0.15648 -11.90 <2e-16 ***

#—

#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

#

#Residual standard error: 0.4585 on 99 degrees of freedom

#Multiple R-squared: 0.5885, Adjusted R-squared: 0.5843

#F-statistic: 141.6 on 1 and 99 DF, p-value: < 2.2e-16

Co zaskakujące, jesteśmy w stanie wyjaśnić 60% wariancji w tym zbiorze danych przy użyciu modelu liniowego – pomimo tego, że wiemy, że naiwny model regresji liniowej jest złym modelem danych falowych. Wiemy również, że dobry model powinien być w stanie wyjaśnić ponad 90% wariancji w tym zbiorze danych, ale nadal chcielibyśmy dowiedzieć się, co zrobił model liniowy, aby uzyskać tak dobre dopasowanie do danych. Aby odpowiedzieć na nasze pytanie, najlepiej wykreślić wyniki dopasowania regresji liniowej przy użyciu naszego preferowanego wariantu geom_smooth, w którym zmuszamy geom_smooth do użycia modelu liniowego, ustawiając metodę opcji = „lm”:

ggplot(data.frame(X = x, Y = y), aes(x = X, y = Y)) +

geom_point() +

geom_smooth(method = ‘lm’, se = FALSE)

Patrząc na rysunek

widzimy, że model liniowy znajduje sposób na uchwycenie połowy struktury fali sinusoidalnej za pomocą linii opadającej w dół. Ale to nie jest świetna strategia, ponieważ systematycznie lekceważysz te części danych, które nie są opisane przez tę nachyloną w dół linię. Jeśli fala sinusoidalna zostanie przedłużona o kolejny okres, R² dla tego modelu nagle spadnie coraz bliżej 0%. Możemy wywnioskować, że domyślny model regresji liniowej przekracza dziwactwa naszego konkretnego zestawu danych i nie znajduje swojej prawdziwej podstawowej struktury falowej. Ale co, jeśli damy algorytmowi regresji liniowej więcej danych wejściowych do pracy? Czy znajdzie strukturę, która faktycznie jest falą? Jednym ze sposobów na to jest przestrzeganie logiki, którą wykorzystaliśmy na początku tego rozdziału i dodanie nowych funkcji do naszego zestawu danych. Tym razem dodamy zarówno drugą potęgę x, jak i trzecią potęgę x, aby dać sobie więcej możliwości poruszania się. Jak widać tutaj, ta zmiana znacznie poprawia naszą moc predykcyjną:

df <- transform(df, X2 = X ^ 2)

df <- transform(df, X3 = X ^ 3)

summary(lm(Y ~ X + X2 + X3, data = df))

#Call:

#lm(formula = Y ~ X + X2 + X3, data = df)

#

#Residuals:

# Min 1Q Median 3Q Max

#-0.32331 -0.08538 0.00652 0.08320 0.20239

#

#Coefficients:

# Estimate Std. Error t value Pr(>|t|)

#(Intercept) -0.16341 0.04425 -3.693 0.000367 ***

#X 11.67844 0.38513 30.323 < 2e-16 ***

#X2 -33.94179 0.89748 -37.819 < 2e-16 ***

#X3 22.59349 0.58979 38.308 < 2e-16 ***

#—

#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

#

#Residual standard error: 0.1153 on 97 degrees of freedom

#Multiple R-squared: 0.9745, Adjusted R-squared: 0.9737

#F-statistic: 1235 on 3 and 97 DF, p-value: < 2.2e-16

Dodając jeszcze dwa dane wejściowe, przeszliśmy z R² 60% do R² 97%. To ogromny wzrost. Zasadniczo nie ma powodu, dla którego nie możemy przestrzegać tej logiki tak długo, jak chcemy, i dodawać kolejne moce X do naszego zestawu danych. Ale gdy dodamy więcej mocy, w końcu zaczniemy mieć więcej danych wejściowych niż punktów danych. Jest to zwykle niepokojące, ponieważ oznacza, że ​​możemy w zasadzie idealnie dopasować nasze dane. Ale wcześniej pojawi się bardziej subtelny problem z tą strategią: nowe kolumny, które dodajemy do naszych danych, są tak podobne pod względem wartości do oryginalnych kolumn, że po prostu przestaną działać. W wynikach podsumowania pokazanych poniżej zobaczysz, że problem został rozwiązany jako „osobliwość”.

df <- transform(df, X4 = X ^ 4)

df <- transform(df, X5 = X ^ 5)

df <- transform(df, X6 = X ^ 6)

df <- transform(df, X7 = X ^ 7)

df <- transform(df, X8 = X ^ 8)

df <- transform(df, X9 = X ^ 9)

df <- transform(df, X10 = X ^ 10)

df <- transform(df, X11 = X ^ 11)

df <- transform(df, X12 = X ^ 12)

df <- transform(df, X13 = X ^ 13)

df <- transform(df, X14 = X ^ 14)

df <- transform(df, X15 = X ^ 15)

summary(lm(Y ~ X + X2 + X3 + X4 + X5 + X6 + X7 + X8 + X9 + X10 + X11 + X12 + X13 +

X14, data = df))

#Call:

#lm(formula = Y ~ X + X2 + X3 + X4 + X5 + X6 + X7 + X8 + X9 +

# X10 + X11 + X12 + X13 + X14, data = df)

#

#Residuals:

# Min 1Q Median 3Q Max

#-0.242662 -0.038179 0.002771 0.052484 0.210917

#

#Coefficients: (1 not defined because of singularities)

# Estimate Std. Error t value Pr(>|t|)

#(Intercept) -6.909e-02 8.413e-02 -0.821 0.414

#X 1.494e+01 1.056e+01 1.415 0.161

#X2 -2.609e+02 4.275e+02 -0.610 0.543

#X3 3.764e+03 7.863e+03 0.479 0.633

#X4 -3.203e+04 8.020e+04 -0.399 0.691

#X5 1.717e+05 5.050e+05 0.340 0.735

#X6 -6.225e+05 2.089e+06 -0.298 0.766

#X7 1.587e+06 5.881e+06 0.270 0.788

#X8 -2.889e+06 1.146e+07 -0.252 0.801

#X9 3.752e+06 1.544e+07 0.243 0.809

#X10 -3.398e+06 1.414e+07 -0.240 0.811

#X11 2.039e+06 8.384e+06 0.243 0.808

#X12 -7.276e+05 2.906e+06 -0.250 0.803

#X13 1.166e+05 4.467e+05 0.261 0.795

#X14 NA NA NA NA

#

#Residual standard error: 0.09079 on 87 degrees of freedom

#Multiple R-squared: 0.9858, Adjusted R-squared: 0.9837

#F-statistic: 465.2 on 13 and 87 DF, p-value: < 2.2e-16

Problem polega na tym, że nowe kolumny, które dodajemy z coraz większymi potęgami X, są tak skorelowane ze starymi kolumnami, że algorytm regresji liniowej rozpada się i nie może znaleźć współczynników dla wszystkich kolumn osobno. Na szczęście istnieje rozwiązanie tego problemu, które można znaleźć w literaturze matematycznej: zamiast naiwnie dodawać proste potęgi x, dodajemy bardziej skomplikowane warianty x, które działają jak kolejne potęgi x, ale nie są ze sobą skorelowane tak jak x i x ^ 2. Te warianty na potęgach x są nazywane wielomianami ortogonalnymi, 1 i można je łatwo wygenerować za pomocą funkcji poly w R. Zamiast bezpośredniego dodawania 14 potęg x do ramki danych, wystarczy wpisać poly (X, stopień = 14) przekształcić x w coś podobnego do X + X ^ 2 + X ^ 3 + … + X ^ 14, ale z ortogonalnymi kolumnami, które nie wygenerują osobliwości podczas uruchamiania lm. Aby upewnić się, że poly czarna skrzynka działa poprawnie, możesz uruchomić lm z wyjściem z poly i przekonać się, że w rzeczywistości da ci właściwe współczynniki dla wszystkich 14 potęg X:

summary(lm(Y ~ poly(X, degree = 14), data = df))

#Call:

#lm(formula = Y ~ poly(X, degree = 14), data = df)

#

#Residuals:

# Min 1Q Median 3Q Max

#-0.232557 -0.042933 0.002159 0.051021 0.209959

#

#Coefficients:

# Estimate Std. Error t value Pr(>|t|)

#(Intercept) 0.010167 0.009038 1.125 0.2638

#poly(X, degree = 14)1 -5.455362 0.090827 -60.063 < 2e-16 ***

#poly(X, degree = 14)2 -0.039389 0.090827 -0.434 0.6656

#poly(X, degree = 14)3 4.418054 0.090827 48.642 < 2e-16 ***

#poly(X, degree = 14)4 -0.047966 0.090827 -0.528 0.5988

#poly(X, degree = 14)5 -0.706451 0.090827 -7.778 1.48e-11 ***

#poly(X, degree = 14)6 -0.204221 0.090827 -2.248 0.0271 *

#poly(X, degree = 14)7 -0.051341 0.090827 -0.565 0.5734

#poly(X, degree = 14)8 -0.031001 0.090827 -0.341 0.7337

#poly(X, degree = 14)9 0.077232 0.090827 0.850 0.3975

#poly(X, degree = 14)10 0.048088 0.090827 0.529 0.5979

#poly(X, degree = 14)11 0.129990 0.090827 1.431 0.1560

#poly(X, degree = 14)12 0.024726 0.090827 0.272 0.7861

#poly(X, degree = 14)13 0.023706 0.090827 0.261 0.7947

#poly(X, degree = 14)14 0.087906 0.090827 0.968 0.3358

#—

#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

#

#Residual standard error: 0.09083 on 86 degrees of freedom

#Multiple R-squared: 0.986, Adjusted R-squared: 0.9837

#F-statistic: 431.7 on 14 and 86 DF, p-value: < 2.2e-16

Ogólnie rzecz biorąc, poly daje dużą moc ekspresji. Matematycy wykazali, że regresja wielomianowa pozwoli ci uchwycić ogromną różnorodność skomplikowanych kształtów w twoich danych. Ale to niekoniecznie jest dobra rzecz. Jednym ze sposobów przekonania się, że dodatkowa moc zapewniana przez poli może być źródłem problemów, jest przyjrzenie się kształtowi modeli generowanych przez poli w miarę zwiększania parametru stopnia. W poniższym przykładzie generujemy modele przy użyciu poli ze stopniami 1, 3, 5 i 25. Wyniki pokazano w panelach tu

poly.fit <- lm(Y ~ poly(X, degree = 1), data = df)

df <- transform(df, PredictedY = predict(poly.fit))

ggplot(df, aes(x = X, y = PredictedY)) +

geom_point() +

geom_line()

poly.fit <- lm(Y ~ poly(X, degree = 3), data = df)

df <- transform(df, PredictedY = predict(poly.fit))

ggplot(df, aes(x = X, y = PredictedY)) +

geom_point() +

geom_line()

poly.fit <- lm(Y ~ poly(X, degree = 5), data = df)

df <- transform(df, PredictedY = predict(poly.fit))

ggplot(df, aes(x = X, y = PredictedY)) +

geom_point() +

geom_line()

poly.fit <- lm(Y ~ poly(X, degree = 25), data = df)

df <- transform(df, PredictedY = predict(poly.fit))

ggplot(df, aes(x = X, y = PredictedY)) +

geom_point() +

geom_line()

Możemy kontynuować ten proces w nieskończoność, ale patrząc na przewidywane wartości dla naszego modelu wyraźnie widać, że ostatecznie dopasowany kształt nie przypomina już fali, ale zaczyna być zniekształcany przez załamania i skoki. Problem polega na tym, że używamy modelu, który jest potężniejszy niż dane są w stanie obsłużyć. Rzeczy działają dobrze dla mniejszych stopni, takich jak 1, 3 lub 5, ale zaczynają się łamać wokół stopnia 25. Problem, który widzimy, to istota nadmiernego dopasowania. W miarę wzrostu liczby naszych obserwacji możemy pozwolić sobie na zastosowanie mocniejszych modeli. Ale dla każdego określonego zestawu danych zawsze istnieją modele, które są zbyt potężne. Jak możemy zrobić coś, aby to zatrzymać? I w jaki sposób możemy lepiej zrozumieć, co pójdzie nie tak, jeśli damy sobie wystarczająco dużo liny, aby się powiesić? Zaproponujemy odpowiedź na połączenie walidacji krzyżowej i legalizacji, dwóch najważniejszych narzędzi w całym zestawie narzędzi do uczenia maszynowego.

Relacje nieliniowe między kolumnami: poza liniami prostymi

Chociaż powiedzieliśmy ci prawdę , kiedy powiedzieliśmy, że regresja liniowa zakłada, że ​​związek między dwiema zmiennymi jest linią prostą, okazuje się, że możesz również zobaczyć regresję liniową, aby uchwycić relacje, które nie są dobrze opisane linią prostą . Aby pokazać, co mamy na myśli, wyobraź sobie, że masz dane pokazane w panelu A  na rysunku poniżej

Patrząc na ten wykres rozrzutu jest oczywiste, że związek między X i Y nie jest dobrze opisany linią prostą. Rzeczywiście, wykreślenie linii regresji pokazuje nam dokładnie, co pójdzie źle, jeśli spróbujemy użyć linii do przechwycenia wzorca w tych danych; panel B na powyższym rysunku pokazuje wynik. Widzimy, że popełniamy błędy systematyczne w naszych prognozach, jeśli zastosujemy linię prostą: przy małych i dużych wartościach x przekraczamy y, a niedoceniamy średnich wartości x. Najłatwiej to zobaczyć na wykresie resztek, jak pokazano w panelu C na powyższym rysunku.

Na tym wykresie można zobaczyć całą strukturę oryginalnego zestawu danych, ponieważ żadna ze struktur nie jest przechwytywana przez domyślny model regresji liniowej. Korzystając z funkcji geom_smooth ggplot2 bez argumentu metody, możemy dopasować bardziej złożony model statystyczny zwany Uogólnionym modelem addytywnym (w skrócie GAM), który zapewnia płynną, nieliniową reprezentację struktury w naszych danych:

set.seed (1)

x <- seq (-10, 10, przez = 0,01)

y <- 1 – x ⋀ 2 + rnorm (długość (x), 0, 5)

ggplot (data.frame (X = x, Y = y), aes (x = X, y = Y)) +

geom_point () +

geom_smooth (se = FALSE)

Wynik pokazany w panelu D na powyższym rysunku pozwala nam od razu zobaczyć, że chcemy dopasować linię krzywą zamiast linii prostej do tego zestawu danych. Jak więc dopasować jakąś krzywą linię do naszych danych? Tutaj pojawiają się subtelności regresji liniowej: regresja liniowa może pasować tylko do linii na wejściu, ale można tworzyć nowe dane wejściowe, które są nieliniowymi funkcjami oryginalnych danych wejściowych. Na przykład możesz użyć następującego kodu w R, aby utworzyć nowe dane wejściowe na podstawie surowego wejścia x, który jest kwadratem surowego wejścia:

x.squared <- x ^ 2

Następnie możesz narysować y względem nowego wejścia x.squared, aby zobaczyć, jak z twoich danych wyłania się zupełnie inny kształt:

ggplot (data.frame (XSquared = x.squared, Y = y), aes (x = XSquared, y = Y)) + geom_point () + geom_smooth (method = ‘lm’, se = FALSE)

Jak pokazano na rysunku

wykreślenie y względem tego nowego wejścia x.squared daje nam dopasowanie, które wygląda dokładnie jak linia prosta. Zasadniczo przekształciliśmy nasz pierwotny problem nieliniowy w nowy problem, w którym związek między dwoma wejściami naprawdę spełnia założenie liniowości regresji liniowej. Pomysł zastąpienia skomplikowanego problemu nieliniowego prostszym problemem liniowym z wykorzystaniem transformacji danych wejściowych pojawia się wielokrotnie w uczeniu maszynowym. Rzeczywiście, ta intuicja jest istotą sztuczki jądra, którą omówimy później. Aby zobaczyć, jak bardzo ta prosta transformacja do kwadratu poprawia naszą jakość przewidywania, możemy porównać wartości R2 dla regresji liniowych za pomocą xi x.squared:

podsumowanie (lm (y ~ x)) $ r.squared

# [1] 2.973e-06

podsumowanie (lm (y ~ x.squared)) $ r.squared

# [1] 0,9707

Przeszliśmy od rozliczania 0% wariancji do rozliczania 97%. To całkiem spory skok dla tak prostej zmiany w naszym modelu. Ogólnie rzecz biorąc, możemy się zastanawiać, o ile więcej mocy predykcyjnej możemy uzyskać, stosując bardziej ekspresyjne modele o bardziej skomplikowanych kształtach niż linie. Z powodów matematycznych, które wykraczają poza nasz zakres, okazuje się, że można uchwycić zasadniczo każdy rodzaj relacji, która mogłaby istnieć między dwiema zmiennymi przy użyciu bardziej złożonych zakrzywionych kształtów. Jedno podejście do budowania bardziej skomplikowanych kształtów nosi nazwę regresji wielomianowej, którą opiszemy w następnej części. Ale elastyczność zapewniana przez regresję wielomianową nie jest czysto dobrą rzeczą, ponieważ zachęca nas do naśladowania szumu w naszych danych dzięki naszemu dopasowanemu modelowi, a nie tylko prawdziwemu wzorcowi, który chcemy odkryć. Pozostała część  skupi się na dodatkowych formach dyscypliny, które musimy ćwiczyć, jeśli będziemy używać bardziej złożonych narzędzi, takich jak regresja wielomianowa zamiast prostego narzędzia, takiego jak regresja liniowaa

Teraz, gdy przygotowaliśmy Cię do pracy z regresjami, studium przypadku tej części skupi się na użyciu regresji do przewidywania liczby odsłon stron dla 1000 najlepszych stron internetowych w 2011 r. Pięć górnych wierszy tego zestawu danych, które dostarczone nam przez Neila Kodnera, pokazano w tabeli 

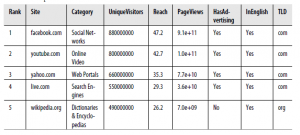
Do naszych celów będziemy pracować tylko z podzbiorem kolumn tego zestawu danych. Skupimy się na pięciu kolumnach: Rank, PageViews, UniqueVisitors, HasAdvertising i IsEnglish.

Kolumna Rank informuje nas o pozycji witryny na pierwszej liście 1000. Jak widać, Facebook jest witryną numer jeden w tym zestawie danych, a YouTube jest drugą. Rank jest interesującym rodzajem pomiaru, ponieważ jest liczbą porządkową, w której liczby są używane nie dla ich prawdziwych wartości, ale po prostu dla ich kolejności. Jednym ze sposobów uświadomienia sobie, że wartości nie mają znaczenia, jest uświadomienie sobie, że nie ma realnej odpowiedzi na pytania typu „Jaka jest 1.578. strona na tej liście?” Tego rodzaju pytanie miałoby odpowiedź, gdyby użyte liczby były wartościami kardynalnymi. Innym sposobem na podkreślenie tego rozróżnienia jest zwrócenie uwagi na rangi 1, 2, 3 i 4 na A, B, C i D i nie utracić żadnych informacji.

Następna kolumna, PageViews, to wynik, który chcemy przewidzieć w tym studium przypadku, i pokazuje nam, ile razy strona była widziana w tym roku. Jest to dobry sposób mierzenia popularności witryn, takich jak Facebook, z wielokrotnie odwiedzanymi użytkownikami, którzy często wracają. Po przeczytaniu całej części dobrym ćwiczeniem byłoby porównanie odsłon strony z UniqueVisitors, aby znaleźć sposób na stwierdzenie, które rodzaje witryn mają wiele powtarzających się odwiedzin, a które z nich mają bardzo niewiele powtórzeń. Kolumna UniqueVisitors mówi nam, ile różnych osób przyszło na stronę w ciągu miesiąca, w którym dokonano tych pomiarów. Jeśli uważasz, że wyświetlenia strony można łatwo zawyżać, powodując, że ludzie niepotrzebnie odświeżają strony, UniqueVisitors to dobry sposób na zmierzenie, ile różnych osób widzi witrynę. Kolumna HasAdvertising informuje nas, czy witryna zawiera reklamy. Możesz pomyśleć, że reklamy byłyby irytujące, a ludzie, wszyscy inni są równi, unikają witryn z reklamami. Możemy to wyraźnie przetestować za pomocą regresji. W rzeczywistości jedną z wielkich wartości regresji jest to, że pozwala ona próbować odpowiadać na pytania, w których musimy mówić o tym, że „wszystko inne jest równe”. Mówimy „spróbuj”, ponieważ jakość regresji jest tak dobra, jak nasze dane wejściowe. Jeśli w naszych danych wejściowych brakuje ważnej zmiennej, wyniki regresji mogą być bardzo dalekie od prawdy. Z tego powodu należy zawsze zakładać, że wyniki regresji są wstępne: „Gdyby dane wejściowe były wystarczające, aby odpowiedzieć na to pytanie, odpowiedź byłaby…”. Kolumna IsEnglish mówi nam, czy strona internetowa jest głównie w języku angielskim. Przeglądając listę, widać, że większość najlepszych witryn to przede wszystkim witryny w języku angielskim lub chińskim. Uwzględniliśmy tę kolumnę, ponieważ interesujące jest pytanie, czy znajomość języka angielskiego jest pozytywna, czy nie. Uwzględniamy również tę kolumnę, ponieważ jest to przykład, w którym kierunek przyczynowości nie jest wcale jasny z regresji; czy pisanie w języku angielskim zwiększa popularność witryny, czy też bardziej popularne witryny decydują się na konwersję na angielski, ponieważ jest to lingua franca w Internecie? Model regresji może powiedzieć, że dwie rzeczy są ze sobą powiązane, ale nie może powiedzieć, czy jedna rzecz powoduje drugą, czy też faktycznie działa odwrotnie. Teraz, gdy opisaliśmy dane wejściowe i zdecydowaliśmy, że PageViews będą naszymi wynikami, zacznijmy rozumieć, w jaki sposób te rzeczy odnoszą się do siebie. Zaczniemy od utworzenia wykresu rozrzutu, który wiąże odsłon strony z UniqueVisitors. Zawsze zalecamy rysowanie wykresów rozrzutu dla zmiennych numerycznych, zanim spróbujesz powiązać je za pomocą regresji, ponieważ wykres rozrzutu może wyjaśnić, kiedy założenie regresji nie jest spełnione.

top.1000.sites <- read.csv(‘data/top_1000_sites.tsv’,

sep = ‘\t’,

stringsAsFactors = FALSE)

ggplot(top.1000.sites, aes(x = PageViews, y = UniqueVisitors)) +

geom_point()

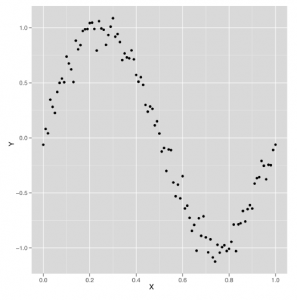
Wykres rozrzutu, który otrzymujemy z tego wywołania do ggplot 

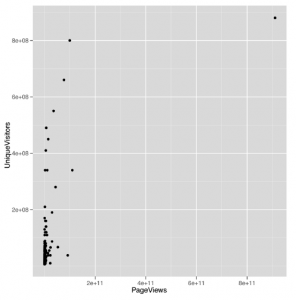
wygląda okropnie:

prawie wszystkie wartości są zebrane razem na osi X i tylko niewielka liczba wyskakuje z paczki. Jest to powszechny problem podczas pracy z danymi, które zwykle nie są dystrybuowane, ponieważ użycie skali wystarczająco dużej, aby pokazać pełny zakres wartości, powoduje, że większość punktów danych jest tak blisko siebie, że nie można ich oddzielić wizualnie. Aby potwierdzić, że kształt danych stanowi problem z tym wykresem, możemy przyjrzeć się rozkładowi odsłon stron:

ggplot(top.1000.sites, aes(x = PageViews)) +

geom_density()

Ten wykres gęstości (pokazany na rysunku 5-7)

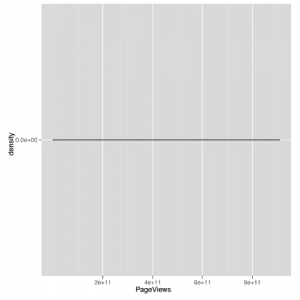
 wygląda tak samo nieprzenikniony jak wcześniejszy wykres rozrzutu. Gdy zobaczysz bezsensowne wykresy gęstości, dobrym pomysłem jest wypróbowanie dziennika wartości, które próbujesz przeanalizować, i wykonanie wykresu gęstości tych wartości przekształconych w log. Możemy to zrobić za pomocą prostego wywołania funkcji dziennika R:

ggplot (top.1000.sites, aes (x = log (PageViews))) +

geom_density ()

Ten wykres gęstości (pokazany na rysunku 5-8)

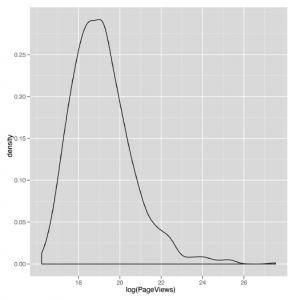
wygląda o wiele bardziej rozsądnie. Z tego powodu odtąd zaczniemy korzystać z przekształconych w dzienniki odsłon strony i UniqueVisitors. Odtworzenie naszego wcześniejszego wykresu rozrzutu na skali dziennika jest łatwe:

ggplot (top.1000.sites, aes (x = log (PageViews), y = log (UniqueVisitors))) +

geom_point ()

Pakiet ggplot2 zawiera również funkcję wygody do zmiany skali osi do dziennika. W takim przypadku możesz użyć dziennika scale_x_log lub scale_y_log. Przypomnijmy również z naszej wcześniejszej dyskusji, że w niektórych przypadkach będziesz chciał użyć funkcji logp w R, aby uniknąć błędów związanych z przyjmowaniem logarytmu zerowego. W tym przypadku jednak nie stanowi to problemu. Powstały wykres rozproszenia pokazany tu

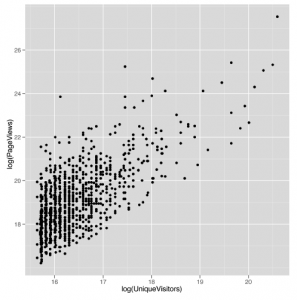
wygląda na to, że istnieje potencjalna linia do narysowania za pomocą regresji. Zanim użyjemy lm do dopasowania linii regresji, użyjmy geom_smooth z argumentem method = ‘lm’, aby zobaczyć, jak będzie wyglądać linia regresji:

ggplot(top.1000.sites, aes(x = log(PageViews), y = log(UniqueVisitors))) +

geom_point() +

geom_smooth(method = ‘lm’, se = FALSE)

Powstała linia, pokazana na rysunku 5-10,

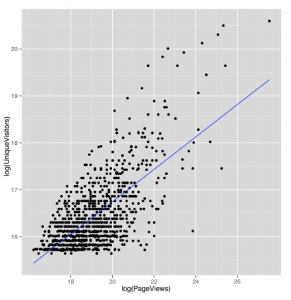
 wygląda obiecująco, więc znajdźmy wartości, które określają jego nachylenie i przechwytują, wywołując lm:

lm.fit <- lm (log (PageViews) ~ log (UniqueVisitors),

data = top.1000.sites)

Teraz, gdy już dopasowaliśmy linię, chcielibyśmy uzyskać jej krótkie podsumowanie. Możemy spojrzeć na współczynniki za pomocą cefe, lub możemy spojrzeć na RMSE za pomocą reszt. Ale wprowadzimy kolejną funkcję, która tworzy znacznie bardziej złożone podsumowanie, które możemy wykonać krok po kroku. Ta funkcja jest dogodnie nazywana summary:

summary(lm.fit)

#Call:

#lm(formula = log(PageViews) ~ log(UniqueVisitors), data = top.1000.sites)

#

#Residuals:

# Min 1Q Median 3Q Max

#-2.1825 -0.7986 -0.0741 0.6467 5.1549

#

#Coefficients:

# Estimate Std. Error t value Pr(>|t|)

#(Intercept) -2.83441 0.75201 -3.769 0.000173 ***

#log(UniqueVisitors) 1.33628 0.04568 29.251 < 2e-16 ***

#—

#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

#

#Residual standard error: 1.084 on 998 degrees of freedom

#Multiple R-squared: 0.4616, Adjusted R-squared: 0.4611

#F-statistic: 855.6 on 1 and 998 DF, p-value: < 2.2e-16

Pierwszą rzeczą, którą mówi nam summary, jest rozmowa z lm. Nie jest to bardzo przydatne, gdy pracujesz przy konsoli, ale może być pomocne, gdy pracujesz w większych skryptach, które wykonują wiele wywołań do lm. W takim przypadku informacje te pomagają w uporządkowaniu wszystkich modeli, dzięki czemu można dokładnie zrozumieć, jakie dane i zmienne trafiły do ​​każdego modelu. Następną rzeczą, którą mówi nam podsumowanie, są kwantyle reszt, które wyliczyłbyś, gdybyś nazwał kwantylem (reszty (lm.fit)). Osobiście nie uważamy tego za bardzo pomocne, chociaż inni wolą szukać symetrii w minimalnej i maksymalnej wartości resztkowej, niż patrzeć na wykres rozrzutu danych. Jednak prawie zawsze uważamy, że wykresy są bardziej pouczające niż streszczenia numeryczne. Następnie podsumowanie mówi nam o współczynnikach regresji o wiele bardziej szczegółowo niż zrobiłby to Coef. Dane wyjściowe z cewki kończą się w tej tabeli jako kolumna „Oszacowanie”. Następnie są kolumny dla „Std. Błąd ”,„ wartość t ”i wartość p każdego współczynnika. Wartości te służą do oceny niepewności, którą mamy w obliczonych przez nas szacunkach; innymi słowy, mają one być miarą naszej pewności, że wartości, które wyliczyliśmy z określonego zestawu danych, są dokładnymi opisami świata rzeczywistego, który wygenerował dane „Std. Błąd ”, na przykład, można wykorzystać do uzyskania 95% przedziału ufności dla współczynnika. Interpretacja tego przedziału może być myląca i czasami jest prezentowana w sposób wprowadzający w błąd. Przedział wskazuje granice, dla których możemy powiedzieć: „95% czasu, algorytm, którego używamy do konstruowania przedziałów, będzie zawierał prawdziwy współczynnik wewnątrz przedziałów, które wytwarza”. Jeśli jest to dla ciebie niejasne, to normalne: analiza niepewności jest niezwykle ważna, ale o wiele trudniejsza niż inne materiały, które omawiamy .Jeśli naprawdę chcesz zrozumieć ten materiał, zalecamy kupienie odpowiedniego podręcznika statystyki. Na szczęście tego rodzaju jakościowe rozróżnienia, które wymagają zwrócenia uwagi na standardowe błędy, zwykle nie są konieczne, jeśli próbujesz po prostu zhakować modele, aby coś przewidzieć. Zarówno „wartość t”, jak i wartość p (zapisane jako „Pr (> | t |)” w danych wyjściowych ze streszczenia) są miarami tego, jak jesteśmy pewni, że prawdziwy współczynnik nie jest równy zero. Mówi się o tym, że jesteśmy przekonani, że istnieje rzeczywisty związek między wynikami a danymi wejściowymi, które obecnie badamy. Na przykład tutaj możemy użyć kolumny „wartość t”, aby ocenić, czy jesteśmy pewni, że Wyświetlenia strony naprawdę są powiązane z UniqueVisitors. Naszym zdaniem te dwie liczby mogą być przydatne, jeśli rozumiesz, jak z nimi pracować, ale są one wystarczająco skomplikowane, aby ich użycie pomogło ludziom założyć, że nigdy nie w pełni rozumieją statystyki. Jeśli zależy ci na tym, aby mieć pewność, że dwie zmienne są ze sobą powiązane, sprawdź, czy oszacowanie wynosi co najmniej dwa standardowe błędy od zera. Na przykład współczynnik log (UniqueVisitors) wynosi 1,33628, a błąd standardowy wynosi 0,04568. Oznacza to, że współczynnik wynosi 1,33628 / 0,04568 == 29,25306 błędów standardowych od zera. Jeśli dzieli Cię więcej niż trzy standardowe błędy od zera, możesz mieć pewność, że Twoje dwie zmienne są powiązane. Wartości t i p są przydatne przy podejmowaniu decyzji, czy związek między dwiema kolumnami w danych jest prawdziwy, czy tylko przypadkiem. Decyzja o istnieniu związku jest cenna, ale zrozumienie związku to zupełnie inna sprawa. Regresje nie mogą ci w tym pomóc. Ludzie próbują je zmusić, ale ostatecznie, jeśli chcesz zrozumieć powody, dla których dwie rzeczy są ze sobą powiązane, potrzebujesz więcej informacji niż zwykła regresja.

Tradycyjnym punktem odcięcia dla pewności, że dane wejściowe są powiązane z naszymi wynikami, jest znalezienie współczynnika oddalonego od zera co najmniej o dwa standardowe błędy. Następną informacją, którą wypluwa podsumowanie, są kody istotności współczynników. Są to gwiazdki pokazane wzdłuż boku, które mają wskazywać, jak duża jest „wartość t” lub jak mała jest wartość p. W szczególności gwiazdka mówi ci niezależnie od tego, czy minął szereg arbitralnych wartości odcięcia, przy których wartość p jest mniejsza niż 0,1, mniejsza niż 0,05, mniejsza niż 0,01 lub mniejsza niż 0,001. Nie martw się o te wartości; są niepokojąco popularne w środowisku akademickim, ale tak naprawdę są reliktami z czasów, gdy analiza statystyczna była wykonywana ręcznie, a nie na komputerze. W tych liczbach nie ma dosłownie żadnej interesującej treści, która nie zostałaby znaleziona w pytaniu, ile standardowych błędów szacuje się od 0. Rzeczywiście, mogliśmy zauważyć w naszym wcześniejszym obliczeniu, że „wartość t” dla log (UniqueVisitors) była dokładnie liczbą standardu błędu od 0, że współczynnik log (UniqueVisitors) był. Ta zależność między wartościami t a liczbą błędów standardowych od zera jest na ogół prawdziwa, dlatego sugerujemy, aby w ogóle nie pracować z wartościami p. Ostateczne informacje, które otrzymujemy, są związane z mocą predykcyjną modelu liniowego, który dopasowaliśmy do naszych danych. Pierwszy element, „resztkowy błąd standardowy”, jest po prostu RMSE modelu, który moglibyśmy obliczyć za pomocą qrt (średnia (reszty (lm.fit) ^ 2)). „Stopnie swobody” odnoszą się do pojęcia, że ​​efektywnie wykorzystaliśmy dwa punkty danych w naszej analizie, dopasowując dwa współczynniki: punkt przecięcia i współczynnik log (UniqueVisitors). Ta liczba, 998, jest istotna, ponieważ niski współczynnik RMSE nie jest imponujący, jeśli użyłeś 500 współczynników w swoim modelu, aby dopasować 1000 punktów danych. Korzystanie z wielu współczynników, gdy masz bardzo mało danych, jest formą nadmiernego dopasowania, o której powiemy więcej później. Następnie widzimy „wielokrotne R-kwadrat”. Jest to standardowy „R-kwadrat”, który opisaliśmy wcześniej, który mówi nam, jaki procent wariancji w naszych danych został wyjaśniony przez nasz model. Tutaj wyjaśniamy 46% wariancji przy użyciu naszego modelu, czyli całkiem dobre.

„Skorygowany R-kwadrat” to druga miara, która penalizuje „Wiele R-kwadrat” za liczbę użytych współczynników. W praktyce osobiście ignorujemy tę wartość, ponieważ uważamy, że jest ona nieco ad hoc, ale jest wielu ludzi, którzy bardzo ją lubią. Wreszcie ostatnia informacja, którą zobaczysz, to „Statystyka F.” Jest to miara ulepszenia twojego modelu w porównaniu z wykorzystaniem jedynie średniej do prognozowania. Jest to alternatywa dla „R-kwadrat”, która pozwala obliczyć „wartość p”. Ponieważ uważamy, że „wartość p” jest zwykle zwodnicza, zachęcamy was, abyście nie pokładali zbyt dużej wiary w statystykę F. „Wartości p” mają swoje zastosowanie, jeśli całkowicie rozumiesz mechanizm zastosowany do ich obliczenia, ale w przeciwnym razie mogą zapewnić fałszywe poczucie bezpieczeństwa, które sprawi, że zapomnisz, że złotym standardem wydajności modelu jest moc predykcyjna danych, które nie były używane do dopasowania modelu, a nie jego wydajności w stosunku do danych, do których był dopasowany. Omówimy metody oceny zdolności Twojego modelu do przewidywania nowych danych w rozdziale 6. Te dane wyjściowe z podsumowania prowadzą nas dość daleko, ale chcielibyśmy zawrzeć inne rodzaje informacji poza powiązaniem odsłon strony z UniqueVisitors. Uwzględnimy także HasAdvertising i IsEnglish, aby zobaczyć, co się stanie, gdy damy naszemu modelowi więcej danych do pracy:

lm.fit <- lm(log(PageViews) ~ HasAdvertising + log(UniqueVisitors) + InEnglish,

data = top.1000.sites)

summary(lm.fit)

#Call:

#lm(formula = log(PageViews) ~ HasAdvertising + log(UniqueVisitors) +

# InEnglish, data = top.1000.sites)

#

#Residuals:

# Min 1Q Median 3Q Max

#-2.4283 -0.7685 -0.0632 0.6298 5.4133

#

#Coefficients:

# Estimate Std. Error t value Pr(>|t|)

#(Intercept) -1.94502 1.14777 -1.695 0.09046 .

#HasAdvertisingYes 0.30595 0.09170 3.336 0.00088 ***

#log(UniqueVisitors) 1.26507 0.07053 17.936 < 2e-16 ***

#InEnglishNo 0.83468 0.20860 4.001 6.77e-05 ***

#InEnglishYes -0.16913 0.20424 -0.828 0.40780

#—

#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

#

#Residual standard error: 1.067 on 995 degrees of freedom

#Multiple R-squared: 0.4798, Adjusted R-squared: 0.4777

#F-statistic: 229.4 on 4 and 995 DF, p-value: < 2.2e-16

Ponownie widzimy, że summary przypomina nasze wezwanie do lm i wypisuje resztki. Nowością w tym podsumowaniu są współczynniki dla wszystkich zmiennych, które uwzględniliśmy w naszym bardziej skomplikowanym modelu regresji. Ponownie widzimy przecięcie wydrukowane jako (Inter cept). Następny wpis jest zupełnie inny niż wszystko, co widzieliśmy wcześniej, ponieważ nasz model zawiera teraz czynnik. Gdy użyjesz współczynnika w regresji, model musi zdecydować o dołączeniu jednego poziomu jako części przechwytywania, a drugiego poziomu jako czegoś, co ma być modelowane jawnie. Tutaj możesz zobaczyć, że HasAdvertising został zamodelowany w taki sposób, że strony, dla których HasAdvertising == „Tak” są oddzielone od przechwytywania, podczas gdy strony, dla których HasAdvertising == „Nie” są składane do przechwytywania. Innym sposobem na opisanie tego jest stwierdzenie, że przechwytywanie jest prognozą dla witryny, która nie ma reklam i ma zerowy dziennik (UniqueVisitors), co faktycznie występuje, gdy masz jednego UniqueVisitor. Możemy zobaczyć tę samą logikę dla InEnglish, z wyjątkiem tego, że ten czynnik ma wiele wartości NA, więc tak naprawdę istnieją trzy poziomy tej zmiennej zastępczej: NA, „Nie” i „Tak”. W takim przypadku R traktuje wartość NA jako domyślną wartość zagięcia do przechwytu regresji i pasuje do oddzielnych współczynników dla poziomów „Nie” i „Tak”. Teraz, gdy zastanowiliśmy się, w jaki sposób możemy wykorzystać te czynniki jako dane wejściowe do naszego modelu regresji, porównajmy każde z trzech danych wejściowych, które wykorzystaliśmy osobno, aby zobaczyć, która z nich ma najbardziej przewidywalną moc, gdy jest używana samodzielnie. Aby to zrobić, możemy wyodrębnić R-kwadrat dla każdego podsumowania osobno:

lm.fit <- lm(log(PageViews) ~ HasAdvertising,

data = top.1000.sites)

summary(lm.fit)$r.squared

#[1] 0.01073766

lm.fit <- lm(log(PageViews) ~ log(UniqueVisitors),

data = top.1000.sites)

summary(lm.fit)$r.squared

#[1] 0.4615985

lm.fit <- lm(log(PageViews) ~ InEnglish,

data = top.1000.sites)

summary(lm.fit)$r.squared

#[1] 0.03122206

pasuje do oddzielnych współczynników dla poziomów „Nie” i „Tak”. Teraz, gdy zastanowiliśmy się, w jaki sposób możemy wykorzystać te czynniki jako dane wejściowe do naszego modelu regresji, porównajmy każde z trzech wejść, które wykorzystaliśmy osobno, aby zobaczyć, która z nich ma najbardziej przewidywalną moc, gdy jest używana samodzielnie. Aby to zrobić, możemy wyodrębnić R-kwadrat dla każdego podsumowania osobno:

lm.fit <- lm(log(PageViews) ~ HasAdvertising,

data = top.1000.sites)

summary(lm.fit)$r.squared

#[1] 0.01073766

lm.fit <- lm(log(PageViews) ~ log(UniqueVisitors),

data = top.1000.sites)

summary(lm.fit)$r.squared

#[1] 0.4615985

lm.fit <- lm(log(PageViews) ~ InEnglish,

data = top.1000.sites)

summary(lm.fit)$r.squared

#[1] 0.03122206

Jak widać, HasAdvertising wyjaśnia tylko 1% wariancji, UniqueVisitors wyjaśnia 46%, a InEnglish wyjaśnia 3%. W praktyce warto uwzględnić wszystkie dane wejściowe w modelu predykcyjnym, gdy są one tanie w zakupie, ale gdyby HasAdvertising był trudny do nabycia programowo, zalecamy umieszczenie go w modelu z innymi danymi wejściowymi, które mają o wiele większą moc predykcyjną