IX.Uzasadnienie i podejmowanie decyzji
Wprowadzenie
Rozumowanie i podejmowanie decyzji są podstawowymi elementami podejścia AI do reprezentacji wiedzy i rozumowania (KR&R). KR&R zajmuje się projektowaniem, analizą i wdrażaniem algorytmów wnioskowania i struktur danych. Praca w KR&R ma głębokie korzenie w rzeczywistości: problemy z rozumowaniem powstają naturalnie w wielu aplikacjach, które wchodzą w interakcje ze światem - rozsądne odpowiedzi na zapytania, diagnoza rozwiązywania problemów, planowanie, rozumowanie wiedzy naukowej, przetwarzanie języka naturalnego i kontrola wielu agentów, wymienić kilka. Oprócz oczywistego znaczenia praktycznego, algorytmy wnioskowania i reprezentacje wiedzy stanowią podstawę teoretycznych badań AI na poziomie ludzkim. Rozumowanie to podpola KR&R poświęcona odpowiadaniu na pytania z różnych danych bez interwencji człowieka lub pomocy. Zazwyczaj dane są podawane w jakimś formalnym systemie, którego semantyka jest jasna. We wczesnych dekadach skoncentrowanych badań nad automatycznym rozumowaniem i udzielaniem odpowiedzi na pytania (od lat 50. XX wieku) dane były w większości podobne do wiedzy lub naszych intuicji na ten temat. Niedawno (od lat 80.) ludzie zakładają, że dane związane z rozumowaniem są mieszanką prostych danych i bardziej złożonych danych. Te pierwsze wymagają niskiego stopnia złożoności obliczeniowej i są przedmiotem badań dużych baz danych (np. relacyjnych baz danych, takich jak te rejestrujące transakcje sprzedaży w firmach, oprogramowanie księgowe dla osób fizycznych oraz ewidencja przedmiotów w sklepach). Te ostatnie są podane w bardziej wyrazistym języku, zajmując mniej miejsca do przedstawienia, i odpowiadają zarówno uogólnieniu, jak i drobniejszej informacji. Podejmowanie decyzji jest formą rozumowania, która koncentruje się na odpowiadaniu na pytania dotyczące preferencji między czynnościami, na przykład w kontekście autonomicznego agenta próbującego wykonać zadanie dla człowieka. Często podejmowanie decyzji odbywa się w dynamicznej dziedzinie, która zmienia się wraz z wykonywaniem działań i upływem czasu. W takich domenach wcześniejsze działania wpływają na późniejsze decyzje, a zadaniem rozumowania jest znalezienie sekwencji działań lub uniwersalnego planu (polityki) reagowania na sytuacje lub wkład sensoryczny. Podejmowane tam decyzje obejmują osiągnięcie celów lub optymalizację niektórych kryteriów, takich jak długość planu, koszt działań lub oczekiwana nagromadzona nagroda w przyszłości. Badania nad dwoma tematami rozumowania i podejmowania decyzji są często przeprowadzane w oderwaniu, przy użyciu różnych metod i różnych teoretycznych ustaleń dla tych dwóch tematów, a ten rozdział przeglądowy podzielony jest według podobnych linii. W rozdziale tym wyróżniono również badania według linii reprezentacji, ze szczególnym naciskiem na reprezentacje oparte na logice i prawdopodobieństwie. Jednak badania nad tymi dwoma tematami mają również znaczący wpływ na wzajemne nawożenie i transfer najważniejszych wyników, technik i pomysłów, a przegląd ten ma szerszą perspektywę, że oba problemy są zasadniczo takie same. Ten rozdział ma na celu zarówno przegląd bieżących badań, jak i omówienie aktualnych i pojawiających się pytań w tej dziedzinie. Obie perspektywy zostały przedstawione razem, starając się zapewnić im równy nacisk. Oczywiście obie perspektywy są poważnie ograniczone. Istnieje ponad 100 000 artykułów i książek na temat rozumowania i podejmowania decyzji, a ponad 3000 artykułów jest publikowanych każdego roku i nieuchronnie wiele szczegółów technicznych i duże wysiłki badawcze nie mogą być tutaj uwzględnione.
Reprezentacja wiedzy i rozumowanie
Od samego początku pola sztucznej inteligencji jednym z dominujących poglądów na ścieżkę rozwiązania problemu sztucznej inteligencji było poszukiwanie wyraźnej reprezentacji dla wiedzy o danym systemie i uzasadnienia na jego temat. Lata 60. przyniosły wiele sukcesów w tym podejściu, znanym później jako KR&R. Znaczna część wysiłków została poświęcona logice pierwszego rzędu (FOL) jako ogólnemu językowi reprezentacji wiedzy oraz dowodom twierdzeń FOL jako generatorów inteligentnego zachowania. W latach 70. podniecenie ustąpiło po odkryciu kilku przeszkód. Te przeszkody obejmowały złożoność rozumowania z FOL, kruchość systemów eksperckich, trudność w reprezentowaniu codziennej wiedzy opartej na zdrowym rozsądku oraz problemy FOL w reprezentowaniu przeskakiwania do wniosków lub rozumowanie z domyślnymi. Lata 80. XX w. Dodatkowo uwypukliły lukę między KR&R a badaniami nad uczeniem maszynowym, teorią sterowania i teorią decyzji. Kolejne badania w KR&R miały na celu rozwiązanie tych problemów na dwa sposoby: zrozumienie, jak przezwyciężyć trudności obliczeniowe z FOL oraz zrozumienie, w jaki sposób budować użyteczne reprezentacje zjawisk w świecie rzeczywistym. FOL jest obliczeniowo równoważny maszynie Turinga, a zatem jest w stanie reprezentować wszystko, co obecne komputery mogą obliczyć. Ta ekspresja reprezentacji jest również powodem, dla którego obliczenia są trudne, ponieważ FOL musi długo obliczać wiele zapytań i może nigdy nie zakończyć obliczeń dla innych. Badania nad językami reprezentacyjnymi, które pozwalają na łatwe odpowiedzi na zapytania, przyniosły wyspecjalizowane języki z dużą ilością aplikacji. W tej sekcji opisano pracę wzdłuż tych ścieżek badawczych, koncentrując się na logicznym rozumowaniu, probabilistycznym i zdrowym rozsądku.
Logika i kombinatoryka
Logika matematyczna (odtąd logika) służy jako formalna podstawa wielu zastosowań w świecie rzeczywistym: komputerów i teorii obliczeniowej, naszego systemu prawnego i argumentacji, a także rozwoju teoretycznego i dowodów w nauce i inżynierii. Współczesna logika zrodziła się z wysiłków przedstawiania codziennych argumentów i rozumowania w sposób kompletny i niepodważalny. Wysiłki KR&R koncentrowały się na rozszerzeniu tej wizji na wykonalny automatyczny program komputerowy. W tej wizji rozumujący reprezentuje swoją wiedzę o świecie w logice, a powody tej wiedzy za pomocą ogólnych algorytmów wnioskowania. Szczegóły tego programu okazały się trudne w kilku formach. Po pierwsze, niektóre rodzaje wiedzy (np. Wiedza przestrzenna, czasowa i niepewna) okazują się trudne do przedstawienia w języku sentymentalnym. Po drugie, nie jest łatwo skompilować potrzebną wiedzę dla dużych aplikacji, ani nie jest łatwo nauczyć się wiedzy w ekspresyjnym logicznym języku. Wreszcie nie jest wykonalne obliczeniowo ani łatwe do uzasadnienia za pomocą ekspresyjnych języków, które wydają się potrzebne, nawet jeśli można pokonać dwie pierwsze trudności (Tseitin 1970). Trzy krytyczne toczące się debaty na ten temat to: Po pierwsze, twierdzenie, że logika nie może reprezentować wielu rzeczy, takich jak analogia, przestrzeń, kształt, niepewność, a zatem nie należy brać ich pod uwagę za aktywną rolę w budowaniu pełnej skali sztucznej inteligencji na poziomie ludzkim system. Kontrargument sugeruje, że logika może służyć jako jedno z kilku narzędzi. Obecnie kombinacja siły reprezentacji, elastyczności i przejrzystości nie jest porównywana z żadną inną metodą lub systemem. Druga krytyczna debata dotyczy twierdzenia, że logika jest zbyt wolna, aby wnioskować, i tak też będzie ,że nigdy nie gra roli we wdrożonym systemie. Roszczenie wzajemne jest takie, że istnieją sposoby przybliżenia wnioskowania za pomocą logiki, tak aby była ona zgodna z ograniczeniami czasowymi, a postępy w przyspieszaniu wnioskowania logicznego. Wreszcie, niektórzy twierdzą, że bardzo trudno jest stworzyć systemy logicznych aksjomatów dla znacznych rzeczywistych aplikacji. Ci, którzy wierzą inaczej, rozwijają strumień aktywnych badań nad technikami uczenia się logicznych aksjomatów z tekstu w języku naturalnym i autorów w sieci WWW . Istnieją różne rodzaje logiki; rozważymy niektóre z najważniejszych, w tym logikę zdań, logikę pierwszego rzędu, logikę modalną i logikę niemonotoniczną. Logika zdań jest bardzo prostym i powszechnym językiem formalnej reprezentacji. Reprezentacja wiedzy odbywa się za pomocą symboli zdań (szczególny przypadek zmiennych boolowskich) 1 i łączników zdań, takich jak ∧ (i), ∨ (lub) i ¬ (nie). Na przykład formuła Φ = ¬rain ∨ chmury stwierdza, że jeśli jest deszcz, muszą istnieć chmury. Istnieją cztery typowe zadania wnioskowania z logiczną wiedzą zdań:
(1) Satysfakcja: Czy istnieje model dla Φ? (model dla formuły jest przypisaniem do wszystkich zmiennych, tak że formuła ma wartość PRAWDA); (2) Entailment: Czy Q logicznie wynika z ?? (napisane Φ |= Q dla danej formuły Q);
(3) Liczenie modeli: ile modeli ma Φ ?, i
(4) Ilościowe formuły boolowskie (QBF): zapytania, które przeplatają warunki uwarunkowania niektórych zmiennych i zadowalalność innych zmiennych.
Główną koncepcją w logice klasycznej jest koncepcja pociągania za sobą lub wnioskowania. Relacja składniowa |- oznacza zdolność do mechanicznego wyprowadzania zapytania z zestawu aksjomatów Φ poprzez zastosowanie szeregu kombinacji syntaktycznych i manipulacji formułami zgodnymi z danym zbiorem reguł. Natomiast relacja semantyczna ? (uwikłanie logiczne) dostarcza nam definicji znaczenia uwikłania. Biorąc pod uwagę semantyczną relację między strukturami formalnymi (modelami) a zdaniami logicznymi, definicje uwarunkowań zwykle mówią, że zbiór zdań logicznych pociąga za sobą inne zdanie, jeśli wszystkie modele spełniające każde zdanie tego pierwszego spełniają również to drugie. Na przykład, jeśli wszystkie modele "deszczu" spełniają "rain ∨ clouds", wówczas mówimy, że "rain" logicznie oznacza "rain ∨ clouds". Logika zazwyczaj ma definicje zarówno relacji, jak i twierdzenia o "kompletności", ustanawiające równoważność między tymi dwiema relacjami. Razem umożliwiają obliczenia, czy Φ jest związany z zestawem przesłanek T QBF to formuły zdań z kwantyfikatorami. Reprezentują takie stwierdzenia, jak: "istnieje plan (sekwencja działań), który osiągnie cel niezależnie od stanu początkowego", który można zapisać jako QBF ∃plan ∀s0 cel(do(plan,s0)) , gdzie plan i s0 są reprezentowane jako zestawy zdań logicznych zdania, do jest kodowaniem zdań (z większą liczbą zmiennych zdań) wykonania sekwencji planu działań zaczynającego się od s0, a celem jest formuła zdań na końcowych zmiennych do (plan, s0). Satysfakcja z ograniczeń jest uogólnieniem logiki zdań na zmienne, które nie są logiczne i mogą przyjmować wartości w skończonej dziedzinie. Bieżące badania nad logiką zdań i satysfakcją z ograniczeń koncentrują się na znalezieniu skutecznych rozwiązań dla tych zadań, przy opracowywaniu heurystyki i teoretycznych rozwiązań dla różnych rozkładów problemów. Logika pierwszego rzędu (FOL) rozszerza logikę zdań i składa się z języka, teorii dowodu i semantyki. Przykład powinien wyjaśnić różnicę:
to formuła w FOL, która mówi, że są czasy (∃czas), w których nad Chicago są chmury, ale nie ma deszczu. Tutaj chmury i deszcz są predykatami, to znaczy symbolami oznaczającymi relacje, czas jest zmienną względem bytów (możliwych czasów), Chicago jest stałym symbolem mającym odnosić się do miasta Chicago, USA, a powyżej (x) to symbol funkcji, który ma odnosić się do obszaru powyżej x. Formalnie język FOL ma zestaw symboli stałych obiektowych, zestaw symboli predykatów relacji, zestaw symboli funkcji i zestaw łączników (OR (∨), AND (∧), NOT (¬)), kwantyfikatory (ISTNIEJE (∃), DLA WSZYSTKICH (∀)) i nawiasy jako operatory budynku. Razem wybrany zestaw symboli predykatów, stałych i funkcji nazywany jest sygnaturą języka. Na przykład powyższy wzór Ψ ma sygnaturę < Chicago; chmury, deszcz;> . FOL ma bogatszą interpretację niż logika zdań. Interpretacja to para M =
ma operator modalny believe, który jako argument przyjmuje stały symbol John i FOL w (Sarah, Home). W tym przykładzie operator modalny uważa, że lekceważy wartość prawdy w (Sarah, Home). Być może Sarah nie ma w domu, ale John w to wierzy. Wiele operatorów modalnych używanych w AI oznacza odpowiednio wiedzę i przekonania, K i B. Unikalną możliwością takich języków jest możliwość omawiania przekonań na temat przekonań na temat przekonań i tak dalej. Na przykład można wyrazić (i uzasadnić) przekonanie Sary, że John zna połączenie z sejfem:
Podobnie, biorąc pod uwagę grupę agentów, można przedstawić i uzasadnić przekonania grupy (np. Każdy wie, że John zna połączenie z sejfem) oraz o powszechnej wiedzy (tj. Każdy wie, że każdy wie …). Wreszcie, innym ważnym zastosowaniem logiki modalnej jest zdolność do reprezentowania wymagań i wiedzy w miarę upływu czasu, na przykład w ostateczności. Jest to szczególnie przydatne w formalnej weryfikacji i innych podejściach do zapewnienia poprawności obwodów cyfrowych, protokołów i oprogramowania. Wszystkie omówione powyżej logiki są monotoniczne, to znaczy dodanie wiedzy nigdy nie powoduje, że wyciągamy wnioski. Formalnie, dla wzorów A, B, C, jeśli A |= C, to także A ∧ B |= C, niezależnie od tego, czym jest B. Ta monotoniczność nie ma miejsca w sytuacjach, w których dochodzi się do wniosków bez uprzedzenia, dlatego w ciągu ostatnich trzydziestu do czterdziestu lat pojawiła się dziedzina skupiająca się na wytwarzaniu systemów, które zapewniają właściwe ramy rozumowania w niemonotonicznych formach dotyczących sytuacji świata rzeczywistego. Przykładem takiej niemonotonicznej logiki jest opis, który jest metodą rozumowania niemonotonicznego, która przyjmuje założenia dotyczące minimalizacji niektórych predykatów, jeśli założenia te są zgodne z resztą wiedzy. Na przykład,
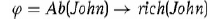
mówi, że John nie jest bogaty, chyba że jest nienormalny. Minimalizowanie predykatu Ab w Φ, tak aby dotyczyło tylko tych rzeczy, o których wiadomo, że są nienormalne, oznacza, że Jan nie jest bogaty. Jeśli dowiemy się teraz, że John zainwestował w Google przed uruchomieniem giełdy, Ab rozszerzy się o Johna i wycofamy ostatni wniosek. Niemonotoniczna linia rozumowania poszerzyła się od czasu swojego debiutu i obecnie istnieje kilka podręczników, które dają rzetelny obraz i jej zastosowań. W badaniu różnych reguł wnioskowania i aksjomatów relacja wnioskowania jest zadowalająca, rozważa się relację wnioskowania jako relację między zbiorem zdań a zdaniem w języku formalnym - zazwyczaj albo w zdaniu, albo w pierwszym rzędzie. Kraus, Lehmann i Magidor (1990) i dalsze prace badają warunki, jakie powinna spełniać ta relacja powiązania, z pewnymi praktycznymi implikacjami. Większość prac na ten temat dotyczyła konkretnych scenariuszy, w szczególności rewizji przekonań . Obecnie głównymi zastosowaniami niemonotonicznych systemów wnioskowania są formalizowanie różnych aspektów rozumowania zdrowego rozsądku i szybka implementacja metod rozumowania w ograniczonych zestawach niemonotonicznych problemów wnioskowania. Tematy aplikacji wykorzystujące te techniki obejmują robotykę kognitywną, planowanie, uczenie się i reprezentowanie preferencji oraz szybkie rozwiązania dla ekspresyjnych rozszerzeń logiki zdań.
Reprezentacje probabilistyczne i rozumowanie
Wiedzę o zjawiskach stochastycznych oraz niepewność dotyczącą wiedzy i przekonań można uchwycić za pomocą narzędzi z teorii prawdopodobieństwa i statystyki. Narzędzia te ułatwiają dyskusję i automatyczne rozumowanie na temat prawdopodobieństwa zdarzeń, przekonań, które możemy utrzymywać, zmian w tych przekonaniach podczas dokonywania obserwacji oraz naszego stopnia pewności w tych przekonaniach. Badania nad tym paradygmatem stały się popularne w ostatnich latach. Badania koncentrują się na reprezentacji różnych rodzajów niepewności i niepewnej wiedzy, rozumowaniu z tymi rodzajami wiedzy i uczeniu się ich. Jest również ściśle związany ze statystycznym podejściem do uczenia maszynowego i teorii sterowania, ułatwiając w ten sposób rozwój stosowanych systemów o znaczeniu praktycznym, takich jak zastosowania w diagnostyce medycznej, sterowanie robotami, widzenie maszynowe i przetwarzanie języka naturalnego. W tej sekcji omówiono główne podejścia i problemy dotyczące tego pola badań. Dotyczy to głównie modeli graficznych rozkładów prawdopodobieństwa i opisuje niektóre podstawowe założenia ich wykorzystania. Te modele graficzne są konstrukcjami matematycznymi opisującymi fragmenty rzeczywistości, z pewnymi założeniami strukturalnymi i parametrami liczbowymi. W tej sekcji omówiono również podejścia do wnioskowania na podstawie tych modeli oraz uczenia się ich parametrów i struktur na podstawie danych. Teoria prawdopodobieństwa opiera się na pojęciu eksperymentu losowego, a mianowicie eksperymentu, którego wynik można przewidzieć z ograniczoną pewnością. Zazwyczaj zakładamy, że eksperyment można powtórzyć w identycznych okolicznościach z identycznymi właściwościami statystycznymi dla wyniku. Założenia te pozwalają na dyskusję, opis i rozumowanie na temat niepewnej wiedzy (np. Uważam, że akcje Facebooka jutro wzrosną z pewnością 0,5) i wiedzy statystycznej (np. 50% dni, kiedy akcje Facebooka zyskują na wartości). Właściwości losowego eksperymentu są rejestrowane przy użyciu zmiennych losowych i rozkładu prawdopodobieństwa. Każda zmienna losowa X jest abstrakcją, która odnosi się do (nieznanego z góry) wyniku (wartości) x losowego eksperymentu. Na przykład zmienna losowa UpFacebook może mieć wartości PRAWDA lub FAŁSZ. Rozkład prawdopodobieństwa P odwzorowuje wartości, które zmienna losowa może przyjmować do segmentu liczb rzeczywistych [0, 1]. W powyższym przykładzie P (UpFacebook = TRUE) = 0,5 wychwytuje oba pojęcia niepewnej wiedzy i wiedzy statystycznej, tylko z różnymi podstawowymi założeniami dotyczącymi znaczenia losowego eksperymentu. Wiele przypadków interesujących społeczność AI dotyczy domen, które są zbyt duże, aby można było je bezpośrednio sprecyzować i uzasadnić. Na przykład, gdy nasza przestrzeń próbki ? dla powyższego przykładu ma n zapasów, Ω ma 2 wartości n. Prosta reprezentacja rozkładu tych wartości ma postać tabeli, w której każdy wiersz jest możliwą kombinacją wartości dla każdego stanu zapasów (np. UpFacebook = True, UpGoogle = False itp.). Tak więc ta tabela miałaby 2n wierszy, a zatem byłaby zbyt duża, aby pomieścić ją w pamięci komputera dla skromnego n = 50. Z tego powodu, od lat 90. badania koncentrowały się na podejściach do kodowania rozkładów prawdopodobieństwa w tak dużych domenach razem z metodami wnioskowania za pomocą tych kodowań. Graficzne modele probabilistyczne (inaczej modele graficzne) są jednym z najpopularniejszych podejść do reprezentowania rozkładów prawdopodobieństwa w takich domenach świata rzeczywistego. Popularna wersja tego podejścia, sieci bayesowskie kodują rozkłady prawdopodobieństwa za pomocą ukierunkowanych wykresów, takich jak na rysunku
Kierowany wykres to zestaw węzłów (kół na tym schemacie) i łączące je strzałki. Każdy węzeł odpowiada losowej zmiennej i zawiera tabelę prawdopodobieństwa warunkowego (CPT) prawdopodobieństwa tej zmiennej losowej, biorąc pod uwagę wartości jej rodziców (węzły wskazujące strzałki w kierunku tej zmiennej). Bayesowska reprezentacja sieci rozkładu prawdopodobieństwa P (X 1, …, X n) reprezentuje go jako iloczyn prawdopodobieństw warunkowych. Zawiera ukierunkowany wykres bez ukierunkowanych cykli, a prawdopodobieństwa warunkowe w produkcie to P (Xi | pai, gdzie pa i są rodzicami Xi. Wynikowa reprezentacja jest znacznie bardziej zwarta niż prosta, ponieważ liczba rodziców zmiennej jest zwykle mniejsza (np. dwa lub trzy) niż całkowita liczba zmiennych, n, co powoduje małe warunkowe tabele prawdopodobieństwa. Czasami sieci bayesowskie są postrzegane jako kodujące związek przyczynowy między funkcjami domeny, na przykład gdy akcje Facebooka
wpływają na stan innej akcji. Przyczynowość ma niewiele wspólnego z matematyczną reprezentacją sieci bayesowskich, ale intuicja przyczynowości wielokrotnie mówi o kierunkach pokazanych w sieci bayesowskiej i jest użyteczną heurystą w budowaniu tych reprezentacji sieci. Istnieje kilka rodzajów zadań związanych z wnioskami z informacjami probabilistycznymi. Typowe zadania to ocena prawdopodobieństwa krańcowego lub warunkowego, znalezienie najbardziej prawdopodobnego przypisania do zmiennych przy danych obserwacjach i generowanie próbek z rozkładu. W przypadku wspólnego rozkładu P (X, Y) marginalna P (X) jest zdefiniowana jako P (X) = ΣY P (X,Y), gdzie X i Y są zestawami zmiennych, a symbol sumowania z indeksem Y oznacza sumowanie wszystkich wartości, które Y może przyjąć. Prawdopodobieństwo krańcowe jest zatem pierwotnym prawdopodobieństwem zastosowanym tylko do podzbioru zmiennych. Na przykład P (wysoki, gruby) jest wspólnym prawdopodobieństwem, że ktoś jest jednocześnie wysoki i gruby, podczas gdy P
(wysoki) jest marginalnym pierwszym, gdy interesuje nas tylko wysoki. Zazwyczaj jesteśmy zainteresowani znalezieniem krańcowego prawdopodobieństwa, że X przyjmie pewną wartość x. Polega to na zsumowaniu wszystkich wartości, które Y może przyjąć. Na przykład, jeśli chcemy znaleźć prawdopodobieństwo, że akcje Facebooka wzrosną, UpFacebook, i mamy wspólny rozkład losowych zmiennych dla wszystkich akcji, musimy zmarginalizować (zsumować) wszystkie zmienne, które nie są Up Facebook. . Pod względem koncepcyjnym obliczanie marginesów jest proste z jego definicji. W praktyce marginalizacja nie jest prosta w przypadku dużych modeli, ponieważ sumowanie może potrwać wykładniczo w liczbie zmiennych, które się sumuje. Z tego powodu wiele badań jest inwestowanych w efektywne obliczanie marginesów. Te badania mogą również służyć do łatwego obliczania innych zadań związanych z rozumowaniem, takich jak znajdowanie najbardziej prawdopodobnych diagnoz medycznych i lokalizowanie robotów. W przypadku sieci
bayesowskich obowiązuje jeden prosty sposób obliczania marginesów i sumowanie zmiennych w sposób ostrożny wzdłuż struktury wykresu. Najpierw podsumowuje zmienne, które mają bardzo niewielu rodziców lub dzieci, najlepiej bez rodziców lub bez dzieci. To podsumowanie tworzy nowy wykres sieci bayesowskiej bez tego węzła, prawdopodobnie tworząc nowe połączenia między rodzicami i dziećmi usuniętego węzła. W ten sposób eliminujemy węzły z wykresu, dopóki nie zostanie nam tylko nasza losowa zmienna zainteresowania na wykresie. Podczas tego iteracyjnego procesu aktualizujemy reprezentację wykresu i CPT w sposób, który nie wymaga więcej niż lokalne obliczenia na przetwarzanie liścia (liść jest węzłem bez dzieci). Jeśli struktura grafu sieci bayesowskiej jest wystarczająco prosta, obliczenia te wymagają czasu, który jest liniowo proporcjonalny do liczby wierzchołków na wykresie (liczba zmiennych w rozkładzie), a także liniowo proporcjonalny do wielkości CPT. Większość praktycznych zastosowań wymaga modeli
probabilistycznych, które są zbyt skomplikowane dla precyzyjnych metod. W takich przypadkach ludzie zwracają się do atrakcyjnego przybliżenia metody rozumowania. Takie metody zapewniają wyniki związane z prawidłowym rozumowaniem, ale z ograniczonymi gwarancjami. Rodzaj przybliżenia rozumowania zależy od zadania i rodziny metod, które stosujemy. Wczesne badania miały na celu znalezienie metod, które zwracają wyniki wnioskowania, które są nieprecyzyjne co najwyżej przez stały czynnik. Niestety wyniki wykazały, że takie przybliżenie nie jest teoretycznie możliwe, chyba że fundamentalne pytanie w informatyce zostanie rozwiązane pozytywnie. Pytanie brzmi, czy znalezienie zadowalającego przypisania w logice zdaniowej może być wykonane w czasie wielomianowym w wielkości problemu wejściowego. Ponieważ uważa się, że nawet przybliżenie wnioskowania probabilistycznego jest twarde, przypieczętowało to dążenie do praktycznych sposobów przybliżenia rozumowania z gwarancjami precyzji. Obecne przybliżone probabilistyczne
techniki wnioskowania są podzielone na dwa główne paradygmaty. Pierwsze przybliżenie wariacyjne próbuje przybliżyć model probabilistyczny z modelem łatwiejszym do obliczenia. Najpopularniejsza technika wykorzystuje formę przekazywania wiadomości, to znaczy przetwarzania dowodów i obserwacji na wykresie oraz wysyłania wiadomości między węzłami na wykresie. Takie komunikaty pomagają zaktualizować lokalne oszacowania marginesów w każdym wierzchołku, a konsekwencje są wykorzystywane do dostarczenia przybliżonych rozwiązań dla tych marginesów. Komunikaty mogą przechodzić na wykresie bez określonej kolejności, choć czasami niektóre zamówienia gwarantują szybszą konwergencję. Drugi paradygmat przybliżonego wnioskowania, techniki Monte Carlo, koncentruje się na zapewnieniu zestawu odpowiedzi na zapytanie, które można wykorzystać do przybliżenia pierwotnego zapytania. Obejmuje to pobieranie próbek. Staramy się generować próbki z podanego rozkładu prawdopodobieństwa i wykorzystujemy je do odpowiedzi na nasze
zapytania. Na przykład w powyższej historii na Facebooku próbkowanie wygeneruje m przykładów (m zależy od czasu, jaki mamy na obliczenia), z których każdy przypisuje wartości do wszystkich zmiennych w modelu - to znaczy każdy przykład określa, czy każdy z n akcji w naszej historii idzie w górę. Bierzemy pod uwagę, ile z tych m próbek odpowiada pozytywnie na nasze zapytanie, i używamy go do zwrócenia przybliżonej odpowiedzi. Uczenie maszynowe to podpola sztucznej inteligencji związana z komputerowym automatycznym uczeniem się z danych wzorców. Celem uczenia maszynowego jest wykorzystanie niektórych danych szkoleniowych do wykrywania wzorców, a następnie wykorzystanie tych wyuczonych wzorców do automatycznego odpowiadania na pytania oraz samodzielnego podejmowania i wykonywania decyzji. Przykładami uczenia maszynowego są modele wyuczone przez komputery w celu przewidywania preferencji użytkowników dotyczących książek, programów telewizyjnych i decyzji zakupowych w sklepach spożywczych. Tam dane szkoleniowe
to książki, które ludzie wybrali w przeszłości oraz cechy tych książek i osób, które je wybrały. Modele wyuczone z tych danych szkoleniowych są następnie wykorzystywane do przewidywania innych książek, które ludzie prawdopodobnie kupiliby. Modele probabilistyczne są zbliżone do statystycznego uczenia maszynowego i służą jako medium między uczeniem maszynowym a automatycznym wnioskowaniem. Uczenie maszynowe modeli probabilistycznych dzieli się na dwa podstawowe zadania: uczenie się CPT po podaniu wykresu i uczenie się samego wykresu. Biorąc pod uwagę przykłady szkolenia, uczenie maszynowe CPT jest stosunkowo łatwe i sprowadza się do zliczenia liczby przypadków, gdy zmienna losowa otrzymuje pewną wartość z czasów, gdy rodzice otrzymali odpowiednie wartości. Ta metoda nazywana jest szacowaniem parametrów według maksymalnego prawdopodobieństwa. Nauka struktury graficznej modelu jest trudniejsza i odbywa się poprzez ulepszanie modelu krok po kroku. Typowe metody stosują algorytm zwany maksymalizacją oczekiwań (EM), który mierzy prawdopodobieństwo, że obecny hipotetyczny model wyjaśnia dane (tj. Że ten model jest w rzeczywistości poprawny i że wygenerował dane treningowe). EM proponuje alternatywne zmiany w modelu i wybiera ten, który najlepiej poprawia objaśnienie danych treningowych. Obecne badania dotyczące reprezentacji probabilistycznej, uczenia się i wnioskowania koncentrują się na zagadnieniach obejmujących dużą liczbę zmiennych (duża tutaj jest większa niż, powiedzmy, 100 zmiennych). Łączne rozkłady ponad 100 zmiennych mogą być bardzo różne, gdy w rzeczywistości (z ludzkiej perspektywy) wydają się niemal identyczne (np. Rozkład cech ulic jednego bloku miasta może być bardzo różny od drugiego, ale mogą wyglądać to samo dotyczy niewytrenowanego oka). Ludzie przyjmują takie założenia, jak niezależność zmiennych losowych, które nie są prawdziwe, co prowadzi do nieprawidłowego postrzegania podobieństwa sytuacji.
Zautomatyzowane podejmowanie decyzji
Podejmowanie decyzji dotyczy podejmowania decyzji, które następnie są wykonywane na świecie przez niezależnego agenta lub przez osobę zasięgającą porady od decydenta. Na przykład agenci gier, autonomiczne roboty, agenci WWW i agenci konwersacji podejmują decyzje, co robić. Często decyzje te uwzględniają dynamikę świata, na przykład gdy komputerowy gracz wybiera akcję opartą na przyszłych możliwych działaniach przeciwnika. Innym razem decyzje są podejmowane bez wyraźnej ścieżki na przyszłość, na przykład kiedy decydujemy się na wynajem mieszkania w określonej cenie i lokalizacji. Podejmowanie decyzji jako obszar badań obejmuje dyscypliny ekonomiczne, psychologiczne, informatyczne i praktycznie wszystkie dyscypliny inżynierskie. W szczególności w informatyce i sztucznej inteligencji badania nad podejmowaniem decyzji koncentrują się na zautomatyzowanych sposobach i właściwościach obliczeniowych procesu decyzyjnego. Oczywiście badania nad podejmowaniem decyzji przez ludzi wpływają na sposób zautomatyzowania procesu decyzyjnego, ale ten aspekt jest poza zakresem sztucznej inteligencji i tego badania. Automatyczne podejmowanie decyzji można podzielić na kilka osi, które można sformułować jako pytania: (1) Czy dziedzina ma charakter dynamiczny, w którym potrzebna jest sekwencja decyzji, lub o charakterze bardziej statycznym, w którym podejmowana jest jedna lub zestaw równoległych decyzji ? Jeśli to pierwsze, czy staramy się optymalizować decyzje dla ograniczonego (małego) zestawu kroków czasowych, czy podejmować (bliskie) optymalne decyzje, które uwzględniają (zasadniczo) nieskończoną przyszłą sekwencję zdarzeń? (2) Czy dziedzina o charakterze deterministycznym, niedeterministycznym czy stochastycznym? Na przykład, czy nasze działania wpływają na świat w sposób deterministyczny (zawsze taki sam, jeśli jest wykonywany w tych samych warunkach) lub stochastyczny (np. W połowie przypadków, gdy nasze działania zawodzą)? (3) Czy próbujemy zoptymalizować narzędzie, czy tylko staramy się osiągnąć cel? (4) Czy dziedzina jest w pełni obserwowana przez cały czas (np. Cały czas widzimy pełny stan szachownicy), czy częściowo obserwowana (np. Nie widzimy czy światło jest włączone w pokoju, chyba że jesteśmy w tym pokoju)? Pozostała część dotyczy podejść do autonomicznego podejmowania decyzji opracowanych w ciągu ostatnich pięćdziesięciu lat. Te techniki zostały opracowane aby być praktyczne, dlatego są wynikiem uproszczenia założeń i decyzji projektowych, których poprawność jest wątpliwa. Założenia te obejmują: wybrane reprezentacje działań deterministycznych (działania mają warunki wstępne i skutki określone przez formuły logiczne); istnienie naprawdę deterministycznych działań w praktyce; poprawna i pełna znajomość modelu świata przez działającego agenta; oraz istnienie wyraźnej funkcji nagrody lub użyteczności, która charakteryzuje nasze wybory. Jednak siłą napędową tych formuł problemów i technik jest często zestaw zastosowań docelowych, więc skuteczność tych założeń jest testowana i sprawdzana w udanych zastosowaniach. Dyskusja dzieli się na podejmowanie decyzji w obszarach logicznych, zazwyczaj deterministycznych i podejmowanie decyzji w domenach o charakterze stochastycznym. Te pierwsze są prostsze, więc można do nich skutecznie podejść pomimo czasami złożonych struktur kombinatorycznych i zazwyczaj można je rozwiązać w przypadku większych domen. Te ostatnie są bardziej skomplikowane w podejmowaniu decyzji, dlatego wymagają wielu założeń, ale są również bardziej skuteczne i lepiej modelują problemy, jeśli mają zastosowanie w praktyce. Później przyjrzymy się pracy, która ma na celu połączenie dwóch podejść i mocnych stron ich metod.
Decyzje w logicznych przestrzeniach kombinatorycznych
Logiczne problemy decyzyjne to te, które mają charakter niestochastyczny. W tej części omówiono dwa główne ustawienia takich problemów decyzyjnych: planowanie (jeden aktor lub współpraca) i kontradyktoryjne (głównie gry dwuosobowe). W obu ustawieniach dyskusja zakłada, że mamy pełną informację o początkowych i pośrednich stanach świata, że działania mają jedynie deterministyczne, znane efekty i że istnieje określony warunek celu (np. wygrana w grze lub pakiet będący w określony pokój). Oba rodzaje problemów dotyczą aktualnych aplikacji w świecie rzeczywistym, takich jak misje kosmiczne NASA, sterowanie robotami, logistyka, oprogramowanie do gier i świata wirtualnego, złożone zachowania w sieci WWW, weryfikacja oprogramowania oraz bezpieczeństwo komputera i sieci. Ogólnie rzecz biorąc, problem planowania obejmuje sytuację początkową, warunek celu oraz zestaw dozwolonych działań lub przejść między stanami. Wynikiem procesu planowania jest sekwencja lub zestaw działań, których prawidłowe wykonanie prowadzi wykonawcę ze stanu początkowego do stanu spełniającego warunek celu. Rozważmy scenariusz, w którym trzy bloki oznaczone A, B, C znajdują się na stole, a chwytak robota musi je podnieść w odpowiedniej kolejności i odłożyć tak, aby A był na B, a B na C. Prosta reprezentacja dla tego scenariusza nazywa się STRIPS i składa się z listy warunków wstępnych, Pre, listy usuwania, Del i listy dodawania, Add, dla każdej akcji robota. Reprezentuje stan z zestawem faktów, które są prawdziwe, i możliwymi działaniami z takimi listami Pre, Add, Del. PASKI mogą reprezentować scenariusz świata bloków za pomocą akcji pickUp (x, y) i putDown (x, y), gdzie x, y to bloki A, B, C lub Tabela. Na przykład pickUp (x, y) może mieć Pre = on (x, y) ?handEmpty, Add = inHand (x) i Del = on (x, y), handEmpty. Intencją tych operatorów i list jest scharakteryzowanie warunków wstępnych i skutków tych działań. Efekt zmienia obecny stan poprzez dodanie i usunięcie go. Kiedy stan świata to {on (A, Table), on (B, Table), on (C, Table) i Puste}, robot podnosi A ze stołu, a następnie A nie jest już na stole, ręka robota nie jest już pusta, a robot trzyma teraz blok A. W związku z tym algorytm planowania aktualizuje stan za pomocą tej akcji, usuwając (A, Tabela), usuwając handEmpty i dodając ręcznie (A) do opisu stanu . Stany i działania określają razem przestrzeń wyszukiwania, w której należy znaleźć plan. Plan w tej przestrzeni jest sekwencją działań, która prowadzi ze stanu początkowego (w pełni określony) do stanu, który spełnia warunek celu. Planista (proces podejmowania decyzji) otrzymuje taką reprezentację dla problemu planowania i ma za zadanie znaleźć plan. W tym celu wykorzystuje różne metody wyszukiwania, które mogą się różnić w zależności od domeny, i mogą obejmować heurystykę ogólnego przeznaczenia, strategie wybiegania w przyszłość i wiedzę w dziedzinie. Planowanie jest trudne obliczeniowo nawet w przypadku prostych języków specyfikacji problemów, takich jak powyższy. Poszukiwanie planu nie może w praktyce reprezentować ani przechodzić przez cały wykres przestrzeni stanu, ponieważ jest on wykładniczo duży pod względem liczby cech stanu definiujących domenę (np. Odpowiadających liczbie bloków w naszym przykładzie powyżej). Dlatego techniki wyszukiwania muszą tworzyć częściowe ścieżki w nadziei na osiągnięcie celu. Poszukiwanie takich planów polega na wycofaniu się, gdy planista zdecyduje, że nie ma sensu dalej rozszerzać planu i że wcześniejsze kroki w planie muszą zostać zmienione, aby umożliwić osiągnięcie celu. Badania nad planowaniem koncentrują się na opracowaniu nowych metod wyszukiwania, nowych reprezentacji działań i stanów, które ułatwiają planowanie oraz bardziej ekspresyjnych języków i metod specyfikacji problemów planowania. Na przykład wiele algorytmów planowania wykorzystuje założenia niezależności lub luźne interakcje między komponentami w dziedzinie planowania, aby efektywniej wyszukiwać plany. Hierarchiczni planiści dzielą cel na podzadania (operatory wysokiego poziomu), wykorzystując rozkład domeny na luźno oddziałujące części. Planowanie odbywa się na każdym poziomie osobno, a następnie plany podrzędne są składane razem, aby zbudować prawidłowy plan. Podejmowanie decyzji, gdy istnieją siły, które próbują negatywnie wpłynąć na nasz wynik, jest tematem teorii gier. Tutaj zadaniem decydenta jest maksymalizacja zysku lub szans na sukces przy jednoczesnym zminimalizowaniu negatywnego efektu decyzji podejmowanych przez innych. Sytuacja ta jest typowa dla gier planszowych dla dwóch graczy (np. Szachy, go itd.), A także jest istotna dla minimalizacji wad w projektach (np. Oprogramowania i sprzętu) oraz dla bezpieczeństwa (np. komputerów i sieci). Minimax jest prostym modelem do podejmowania takich decyzji w sytuacjach dwuosobowych. Decydent wykorzystuje informacje heurystyczne o wartości stanów (według ich przyszłych wyników), aby oszacować wartość decyzji w obecnym stanie. Na przykład w szachach poruszamy pionek szachowy, drugi gracz przesuwa kawałek własny i dochodzimy do nowego stanu gry, który wymaga kolejnej decyzji. Każda nasza decyzja prowadzi do jednego z kilku stanów, podobnie jak decyzja przeciwnika. Możemy nakreślić wszystkie możliwe przyszłe stany kolejnych kroków, patrząc na te stany osiągalne z naszego obecnego stanu poprzez szereg możliwych wyborów przez nas i naszego przeciwnika. Wygodnie jest umieścić te poszczególne stany w drzewie, przy czym stan obecny jest korzeniem tego drzewa (najwyższy węzeł w drzewie), a liście drzewa są najniższymi węzłami w drzewie. (Mówiąc bardziej ogólnie, gałęzie drzewa mogą się łączyć, ale ignorujemy to, aby uprościć dyskusję.) W minimax obliczamy wartości wyższych węzłów zgodnie z tym drzewem w sposób min-max. Poziom drzewa wynosi min (minimalizacja), jeśli przeciwnik podejmie decyzję w tych stanach, ponieważ jego celem jest doprowadzenie do stanów, które minimalizują nasz wynik. Poziom drzewa jest maksymalny (maksymalny), jeśli to my podejmujemy decyzję w tych stanach, ponieważ naszym celem jest doprowadzenie do stanów, które maksymalizują nasz wynik. Ilustruje to rysunek
Na tym rysunku liczby u dołu drzewa oznaczają wartości, które gracze oszacowaliby za bycie w tym stanie (na przykład za pomocą heurystycznego function), a każdy gracz wybiera działania, które minimalizują lub maksymalizują wartości otrzymane od dołu. Prawdopodobnie poprawne metody usuwają gałęzie z drzewa minimax, jeśli nie ma szansy, że przyczynią się do rozwiązania (tj. Preferencji wśród wyższych gałęzi). Najnowsze badania próbują oszacować wartość stanu poprzez próbkowanie sub-drzew tego drzewo min - maks. Wyzwaniem dla przeciwnych decyzji jest wyważenie uczenia się i decyzji. Gdy przeciwnik próbuje zablokować nasze próby, nauka domeny podczas podejmowania decyzji (np. Poprzez naukę wzmacniającą) jest trudna, ponieważ eksploracja w celu uczenia się może doprowadzić nas do bardzo złych wyników. Musimy zrównoważyć prawdopodobieństwo pozyskania cennych informacji z eksploracji z ryzykiem cofnięcia się przez naszych przeciwników. Jednak unikanie eksploracji z pewnością przyniesie nieoptymalne wyniki, które mogą być bardzo dalekie od pożądanych lub akceptowalnych.
Domeny stochastyczne
Wiele domen świata rzeczywistego ma dynamikę, która ewoluuje stochastycznie, to znaczy z pewnymi nietrywialnymi właściwościami statystycznymi. Na przykład możemy rozważyć zakup samochodu, który ma właściwości, które nie są nam znane i wpływają na jego wartość. Te zależności wpływają na naszą decyzję i musimy ocenić naszą użyteczność, biorąc pod uwagę wszystkie ryzyka i niepewności. Domeny stochastyczne są trudniejsze w podejmowaniu decyzji w praktyce, ale są także bardziej tolerancyjne dla przybliżeń niż domeny deterministyczne. Uproszczenie założeń, które zostały poczynione w praktyce, pozwala na automatyczne podejmowanie decyzji. Istnieje kilka sformułowań problemów, które wychwytują różne aspekty i przypadki podejmowania decyzji w domenach stochastycznych. Najważniejsze z nich to sieci decyzyjne i procesy decyzyjne Markowa (MDP). Sieci decyzyjne są podobne do sieci bayesowskich tylko z trzema typami węzłów: (1) zmienne losowe (jak w sieci bayesowskiej), (2) węzły decyzyjne i (3) węzły użyteczności. Węzły decyzyjne wymagają przypisania decyzji co do ich wartości i nie mają rządzącego nimi rozkładu prawdopodobieństwa (wartości dla innych węzłów mogą zależeć stochastycznie od wartości przypisanej do węzłów decyzyjnych). Węzły użytkowe oznaczają ilości, które chcemy zmaksymalizować (w oczekiwaniu). MDP są najbardziej popularnym formalizmem do modelowania zadań decyzyjnych w dynamicznych środowiskach stochastycznych. Ich celem jest modelowanie sytuacji, w których działania mają efekty stochastyczne, a ich cel nie jest konkretnym celem, ale raczej maksymalizuje użyteczność w czasie. Rozwiązania MDP to zasady, które wybierają akcję dla każdego stanu, tak aby całkowity koszt oczekiwanych działań został zminimalizowany, a łączna suma lub dodatnie korzyści zostały zmaksymalizowane.
Zagadnienia przekrojowe
Rozumowanie oparte na zdrowym rozsądku
Terminy "rozumowanie zdrowego rozsądku" i "wiedza zdrowego rozsądku" odnoszą się do szerokiego zestawu umiejętności, które ludzie wnoszą w podejmowanie decyzji i myślenie. Jednym z przykładów jest umiejętność rozumowania o bardzo dużej liczbie przedmiotów, właściwości, ludzi i relacji w naszym codziennym życiu. Możemy stwierdzić, że kubek może utrzymać swoją zawartość, ale tylko wtedy, gdy kubek jest skierowany do góry lub zawartość jest bezpiecznie połączona z kubkiem. Możemy wykorzystać ten fakt przy podejmowaniu decyzji o sposobach transportu kubka z jednego miejsca do drugiego. Badania nad zdrowym rozsądkiem starają się wyposażyć aplikacje i komputery w tę zdolność do generalizowania, uczenia się i korzystania z bardzo szerokiego zestawu wiedzy na temat codziennego życia. Obecnie praktyczne zastosowania omijają wiele problemów związanych z rozsądnym rozumowaniem. Robią to, starannie opracowując potrzebne informacje i modele, ograniczając zestaw tematów i zmiennych podczas uczenia się i opracowywania tylko tych aplikacji, które nie wymagają tak zdrowego rozsądku. Badania nad rozumowaniem opartym na zdrowym rozsądku są podzielone na trzy główne nurty: teoria logiczna, duże podstawy wiedzy o zdrowym rozsądku i techniki rozumowania zwykłego ad hoc. Logiczna formalizacja i teoria rozumowania opartego na zdrowym rozsądku próbuje wykorzystywać i modyfikować logikę do reprezentowania i rozumowania za pomocą wiedzy opartej na zdrowym rozsądku w sposób zgodny z naszymi intuicjami na temat takiego rozumowania. Na przykład wiele ludzkich rozumowań na temat świata używa pojęcia domyślnych - założeń, które są użyteczne, ale mogą nie być prawdziwe. Mówimy, że ptaki latają (niektóre nie); zakładamy, że nasz komputer działa poprawnie (może nie być); i postępujemy zgodnie z zaleceniami lekarzy (mogą być niepoprawni). Takie niepewności i niewykonanie zobowiązań nie są tak samo wychwytywane przez logikę. Rozumowanie niemonotoniczne próbuje uogólnić je na formę użytecznego rozumowania opartego na zdrowym rozsądku. Takie logiki wychwytują jedną właściwość potrzebną do rozsądnego rozumowania, a mianowicie zdolność do reprezentowania wartości domyślnych i rozumowania ich. Pozostaje jednak wiele do zrobienia: w jaki sposób możemy zdobyć wiedzę, w jaki sposób skalujemy techniki reprezentacji i wnioskowania do dużego zestawu wiedzy, który wydaje się potrzebny, i w jaki sposób wykorzystujemy tę wiedzę w aplikacjach, które jej potrzebują? Wysiłki na rzecz budowania dużych baz wiedzy i wykorzystywania informacji w nowy sposób starają się przezwyciężyć ograniczenia logicznego rozumowania opartego na zdrowym rozsądku. Na przykład Cyc, najbardziej znana obecnie duża baza wiedzy opartej na zdrowym rozsądku, jest wynikiem ponad dwudziestu pięciu lat rozwoju i utrzymania przez ekspertów. Zawiera ponad 1 000 000 faktów i zdań logicznych na temat ponad 100 000 obiektów, relacji, typów i funkcji. Jego semantyka nie jest tak prosta i przejrzysta, jak sugerowana w literaturze dotyczącej formuł logicznych, ale wydaje się, że w rezultacie jest bardziej użyteczna (początkowe zastosowania istnieją w przetwarzaniu języka naturalnego i podejmowaniu decyzji). Inne wysiłki podejmowane są w celu automatycznego tworzenia wiedzy na podstawie autorów i mas informacji dostępnych w Internecie. Celem jest łatwiejsze tworzenie systemów o szerokiej wiedzy, ale z możliwie luźniejszą semantyką. Podejścia te unikają rozważania pytań dotyczących znaczenia posiadanej wiedzy i wydają się obiecujące dla aplikacji wymagających szerokiej wiedzy (np. Autonomiczne roboty rzeczywiste i wirtualne).
Połączenie logiki i prawdopodobieństwa
Wiele aplikacji ma zarówno elementy stochastyczne, jak i niestochastyczne. Na przykład sterowanie robotem może obejmować specyfikacje wysokiego poziomu w logice i probabilistyczny model wykrywania niższego poziomu. Ponadto przetwarzanie języka naturalnego ma na celu zastosowanie wiedzy wysokiego poziomu w logice z niższymi modelami probabilistycznymi sygnałów tekstowych i mówionych. Wreszcie, wiele baz danych jest opartych na logice, podczas gdy relacje między tymi bazami danych a najnowszymi rozszerzeniami do baz danych są probabilistyczne (np. Wpis John, Mary jest niepewnym wpisem w bazie danych uwielbia z prawdopodobieństwem 0,7 albo dlatego, że John jest niepewny, albo dlatego, że posiadacze bazy danych nie są pewni). Od 1990 r. W środowisku sztucznej inteligencji i społeczności baz danych jest wiele pracy nad połączeniem ekspresji logicznej i probabilistycznej. W pracy przedstawiono języki, które mogą wyrażać rozkłady prawdopodobieństwa wraz z wyraźnymi odniesieniami do obiektów, funkcji i relacji, jak w logice pierwszego rzędu. Te języki stanowią przydatne ramy dla wielu aplikacji uczenia maszynowego, a ostatnie prace pokazują również, że są przydatne dla wydajności obliczeniowej wnioskowania. Trwają badania nad kombinacją logiki i prawdopodobieństwa. Obecne wyzwania obejmują (1) zastosowanie struktury relacyjnej w celu przyspieszenia wnioskowania i leczenia modeli probabilistycznych na wielu obiektach, (2) połączenie baz wiedzy, które są już podane w postaci probabilistycznej lub logicznej, oraz (3) rozszerzenie języków reprezentacji o funkcje i równość obiekty w dźwięku i proste sposoby.
Częściowa obserwowalność
Agenci działający w wielu rzeczywistych domenach nie znają dokładnego stanu świata w żadnym momencie. Domeny te są częściowo obserwowalne, ponieważ agenci nie mogą obserwować wszystkich cech świata, które mogą być dla nich istotne. Na przykład agent przeglądający strony WWW może nacisnąć przycisk na stronie, ale może nie zobaczyć natychmiastowego efektu jego działania (ale może go zobaczyć, jeśli obejrzał inną stronę). Problemy związane z częściową obserwowalnością są szczególnie trudne, i ograniczone zazwyczaj do bardzo małych domen (np. 100 stanów lub 8 funkcji domenowych). Wynika to z faktu, że każdy wybór działania zależy od stanu wiedzy agenta i odbieranych przez niego spostrzeżeń, co prowadzi do obliczeń nadwykładniczych w liczbie kroków i funkcji w domenie. Działanie w częściowo obserwowalnych, częściowo znanych domenach jest szczególnie trudne, a jednak najbliższe prawdziwemu życiu. Główne podejścia obejmują co najmniej wyczerpujące badanie domeny lub porady na temat obiecujących trajektorii. Podejścia, które gwarantują zbieżność z rozwiązaniem, robią to tylko w nieskończonej liczbie kroków. Co najważniejsze, jeśli zmieni się cel systemu, proces musi zostać zrestartowany, a wiedza zgromadzona w poprzednich uruchomieniach jest mało wykorzystywana. Najnowsze podejścia identyfikują ważne możliwe do prześladowania przypadki o szczególnym znaczeniu - na przykład dziedziny, w których działania są znane jako deterministyczne i pozbawione efektów warunkowych (np. Działania STRIPS. Takie algorytmy przeplatają planowanie i wykonanie oraz zapewniają pewne gwarancje osiągnięcia celu w ramach niemal optymalnej liczby kroków.
Aplikacje nie programują
Dominujący pogląd w badaniach naukowych sugeruje, że rzeczywiste zastosowania są prostymi implementacjami teorii i badań podstawowych. Sztuczna inteligencja i podejmowanie decyzji w szczególności są sprzeczne z tym poglądem. Przetwarzanie języka naturalnego, widzenie maszynowe i wykrywanie oszustw to tylko niektóre aplikacje, które można postrzegać w sposób abstrakcyjny jako aplikacje badań podstawowych. Mimo to te tematy wymagały i otrzymywały (i nadal otrzymują) dużą specjalistyczną uwagę, zanim mogły zostać wprowadzone w życie. Mówiąc bardziej ogólnie, teoretycznie należy umieć przedstawić wszystko, co jest potrzebne do inteligentnego zachowania w FOL. Wynika to z faktu, że FOL odpowiada mocy reprezentacyjnej maszynom Turinga2 (dominujący abstrakcyjny model obliczeń). Podczas gdy sztuczna inteligencja na poziomie ludzkim w FOL jest teoretycznie możliwa (ponieważ jeśli dowolny komputer może to zrobić, to FOL może), w praktyce niewiele można zyskać unikając problemu, jak faktycznie reprezentować wiedzę lub rozum w FOL lub innym języku. Problemów związanych z faktycznym budowaniem potrzebnej wiedzy i wykorzystywaniem jej w praktyce nie da się uniknąć, jeśli chcemy osiągnąć praktyczne inteligentne aplikacje na poziomie człowieka. Diabeł tkwi w szczegółach i bez zwracania uwagi na te szczegóły badania przyniosą niewielkie postępy, co zaobserwowano w licznych gałęziach AI, które rozwijały się w czasie (Formalna Weryfikacja i Bazy Danych to dwie dziedziny, które rozgałęziły się na AI).
Wnioski
Od połowy lat 90. w KR&R nastąpiła znaczna zmiana orientacji z narzędzi matematyczno-logicznych na narzędzia teorii prawdopodobieństwa i z teorii na zastosowania. Ta zmiana była gwałtowna, co doprowadziło do podziału badań na pracę opartą na logice i prawdopodobieństwie. Logika jest wygodniejsza do reprezentowania wiedzy sentymentalnej (szczególnie relacyjnej, opartej na obiektach) i jest dobrze dostosowana do problemów i struktur kombinatorycznych (niewypukłych), takich jak wyszukiwanie w labiryncie lub rozwiązywanie zagadek, podczas gdy podejścia oparte na prawdopodobieństwie (w szczególności , graficzne modele probabilistyczne) lepiej przedstawiają niepewną wiedzę, lepiej nadają się do uczenia się w obecności hałasu i mają wiele rzeczywistych zastosowań (zgodnie z zasadą 80-20 - wykonuj 20% pracy dla łatwiejszego 80% Praca). Rozumowanie i podejmowanie decyzji przy każdym przedstawicielstwie jest łatwiejsze lub trudniejsze w różnych sytuacjach i zazwyczaj ich zalety wydają się komplementarne (np. rozwiązywanie problemów logicznej satysfakcji jest często szybkie, podczas gdy rozumowanie probabilistyczne jest łatwe do przybliżenia). Wielu badaczy zgadza się, że oba narzędzia (logika i prawdopodobieństwo) są niezbędne do skalowania systemów do rzeczywistych aplikacji, ale sposób łączenia ich mocnych stron pozostaje niejasny. Ponadto badania dotyczące uczenia maszynowego i wnioskowania osiągnęły punkt gdzie ma wiele praktycznych zastosowań. Obecne badania są bardziej zorientowane na aplikacje, a trend ten rejestruje lepsze ukierunkowanie i sukcesy w świecie rzeczywistym. Pojawienie się W WW i udanych wyszukiwarek dostarczyło innego rodzaju siły decyzyjnej, gdzie siła kolektywu pomaga uniknąć trudnych problemów teoretycznych. Zmiany te tworzą odmienne środowisko badawcze i kierunki uzasadnienia i podejmowania decyzji. Te nowe kierunki będą oddziaływać z rozwojem teorii gier, neurobiologii i innych dziedzin naukowych, których tu nie poruszono.